Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 145442 by ArielVyny last updated on 04/Jul/21

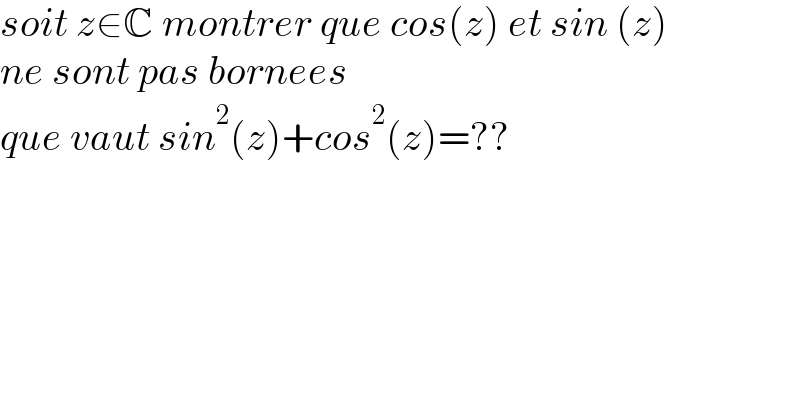
soit z∈C montrer que cos(z) et sin (z) ne sont pas bornees que vaut sin^2 (z)+cos^2 (z)=??

$${soit}\:{z}\in\mathbb{C}\:{montrer}\:{que}\:{cos}\left({z}\right)\:{et}\:{sin}\:\left({z}\right) \\ $$$${ne}\:{sont}\:{pas}\:{bornees} \\ $$$${que}\:{vaut}\:{sin}^{\mathrm{2}} \left({z}\right)+{cos}^{\mathrm{2}} \left({z}\right)=?? \\ $$

Answered by Olaf_Thorendsen last updated on 05/Jul/21

cos(iy) = ((e^(i(iy)) +e^(−i(iy)) )/2) = ((e^(−y) +e^y )/2) = chy sin(iy) = ((e^(i(iy)) −e^(−i(iy)) )/(2i)) = ((e^(−y) −e^y )/(2i)) = ishy cosz = cos(x+iy) cosz = cosxcos(iy)−sinxsin(iy) cosz = cosxchy−isinxshy cosz non borne a cause de chy et shy sinz = sin(x+iy) sinz = sinxcos(iy)+cosxsin(iy) sinz = sinxchy+icosxshy sinz non borne a cause de chy et shy cos^2 z = (cosxchy−isinxshy)^2 cos^2 z = cos^2 xch^2 y−sin^2 xsh^2 y −2icosxsinxchyshy sin^2 z = (sinxchy+icosxshy)^2 sin^2 z = sin^2 xch^2 y−cos^2 xsh^2 y +2icosxsinxchyshy cos^2 z+sin^2 z = cos^2 xch^2 y−sin^2 xsh^2 y +sin^2 xch^2 y−cos^2 xsh^2 y cos^2 z+sin^2 z = (ch^2 y−sh^2 y)(cos^2 x+sin^2 x) cos^2 z+sin^2 z = 1×1 = 1 On retrouve la meme relation fondamentale que pour les reels.

$$\mathrm{cos}\left({iy}\right)\:=\:\frac{{e}^{{i}\left({iy}\right)} +{e}^{−{i}\left({iy}\right)} }{\mathrm{2}}\:=\:\frac{{e}^{−{y}} +{e}^{{y}} }{\mathrm{2}}\:=\:\mathrm{ch}{y} \\ $$$$\mathrm{sin}\left({iy}\right)\:=\:\frac{{e}^{{i}\left({iy}\right)} −{e}^{−{i}\left({iy}\right)} }{\mathrm{2}{i}}\:=\:\frac{{e}^{−{y}} −{e}^{{y}} }{\mathrm{2}{i}}\:=\:{i}\mathrm{sh}{y} \\ $$$$ \\ $$$$\mathrm{cos}{z}\:=\:\mathrm{cos}\left({x}+{iy}\right) \\ $$$$\mathrm{cos}{z}\:=\:\mathrm{cos}{x}\mathrm{cos}\left({iy}\right)−\mathrm{sin}{x}\mathrm{sin}\left({iy}\right) \\ $$$$\mathrm{cos}{z}\:=\:\mathrm{cos}{x}\mathrm{ch}{y}−{i}\mathrm{sin}{x}\mathrm{sh}{y} \\ $$$$\mathrm{cos}{z}\:\mathrm{non}\:\mathrm{borne}\:\mathrm{a}\:\mathrm{cause}\:\mathrm{de}\:\mathrm{ch}{y}\:\mathrm{et}\:\mathrm{sh}{y} \\ $$$$ \\ $$$$\mathrm{sin}{z}\:=\:\mathrm{sin}\left({x}+{iy}\right) \\ $$$$\mathrm{sin}{z}\:=\:\mathrm{sin}{x}\mathrm{cos}\left({iy}\right)+\mathrm{cos}{x}\mathrm{sin}\left({iy}\right) \\ $$$$\mathrm{sin}{z}\:=\:\mathrm{sin}{x}\mathrm{ch}{y}+{i}\mathrm{cos}{x}\mathrm{sh}{y} \\ $$$$\mathrm{sin}{z}\:\mathrm{non}\:\mathrm{borne}\:\mathrm{a}\:\mathrm{cause}\:\mathrm{de}\:\mathrm{ch}{y}\:\mathrm{et}\:\mathrm{sh}{y} \\ $$$$ \\ $$$$\mathrm{cos}^{\mathrm{2}} {z}\:=\:\left(\mathrm{cos}{x}\mathrm{ch}{y}−{i}\mathrm{sin}{x}\mathrm{sh}{y}\right)^{\mathrm{2}} \\ $$$$\mathrm{cos}^{\mathrm{2}} {z}\:=\:\mathrm{cos}^{\mathrm{2}} {x}\mathrm{ch}^{\mathrm{2}} {y}−\mathrm{sin}^{\mathrm{2}} {x}\mathrm{sh}^{\mathrm{2}} {y} \\ $$$$−\mathrm{2}{i}\mathrm{cos}{x}\mathrm{sin}{x}\mathrm{ch}{y}\mathrm{sh}{y} \\ $$$$ \\ $$$$\mathrm{sin}^{\mathrm{2}} {z}\:=\:\left(\mathrm{sin}{x}\mathrm{ch}{y}+{i}\mathrm{cos}{x}\mathrm{sh}{y}\right)^{\mathrm{2}} \\ $$$$\mathrm{sin}^{\mathrm{2}} {z}\:=\:\mathrm{sin}^{\mathrm{2}} {x}\mathrm{ch}^{\mathrm{2}} {y}−\mathrm{cos}^{\mathrm{2}} {x}\mathrm{sh}^{\mathrm{2}} {y} \\ $$$$+\mathrm{2}{i}\mathrm{cos}{x}\mathrm{sin}{x}\mathrm{ch}{y}\mathrm{sh}{y} \\ $$$$ \\ $$$$\mathrm{cos}^{\mathrm{2}} {z}+\mathrm{sin}^{\mathrm{2}} {z}\:=\:\mathrm{cos}^{\mathrm{2}} {x}\mathrm{ch}^{\mathrm{2}} {y}−\mathrm{sin}^{\mathrm{2}} {x}\mathrm{sh}^{\mathrm{2}} {y} \\ $$$$+\mathrm{sin}^{\mathrm{2}} {x}\mathrm{ch}^{\mathrm{2}} {y}−\mathrm{cos}^{\mathrm{2}} {x}\mathrm{sh}^{\mathrm{2}} {y} \\ $$$$\mathrm{cos}^{\mathrm{2}} {z}+\mathrm{sin}^{\mathrm{2}} {z}\:=\:\left(\mathrm{ch}^{\mathrm{2}} {y}−\mathrm{sh}^{\mathrm{2}} {y}\right)\left(\mathrm{cos}^{\mathrm{2}} {x}+\mathrm{sin}^{\mathrm{2}} {x}\right) \\ $$$$\mathrm{cos}^{\mathrm{2}} {z}+\mathrm{sin}^{\mathrm{2}} {z}\:=\:\mathrm{1}×\mathrm{1}\:=\:\mathrm{1} \\ $$$$\mathrm{On}\:\mathrm{retrouve}\:\mathrm{la}\:\mathrm{meme}\:\mathrm{relation} \\ $$$$\mathrm{fondamentale}\:\mathrm{que}\:\mathrm{pour}\:\mathrm{les}\:\mathrm{reels}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com