
Question Number 166379 by SANOGO last updated on 19/Feb/22
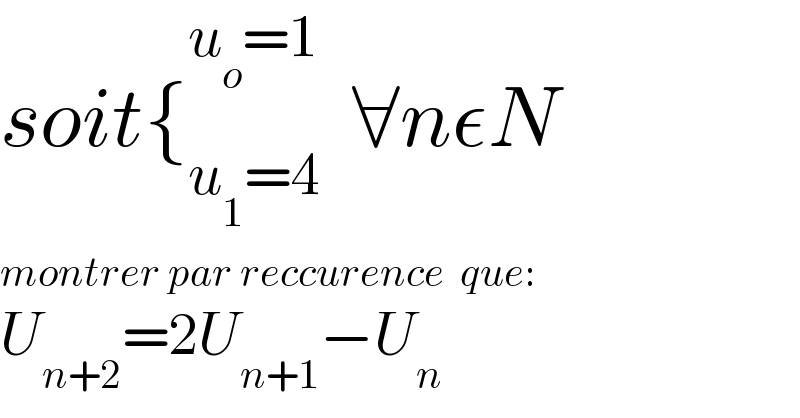
$${soit}\left\{_{{u}_{\mathrm{1}} =\mathrm{4}} ^{{u}_{{o}} =\mathrm{1}} \:\:\forall{n}\epsilon{N}\right. \\ $$$${montrer}\:{par}\:{reccurence}\:\:{que}: \\ $$$${U}_{{n}+\mathrm{2}} =\mathrm{2}{U}_{{n}+\mathrm{1}} −{U}_{{n}} \\ $$
Answered by qaz last updated on 19/Feb/22

$$\mathrm{U}_{\mathrm{n}+\mathrm{2}} =\mathrm{2U}_{\mathrm{n}+\mathrm{1}} −\mathrm{U}_{\mathrm{n}} \\ $$$$\Rightarrow\lambda^{\mathrm{2}} −\mathrm{2}\lambda+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\lambda_{\mathrm{1}} =\lambda_{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\mathrm{U}_{\mathrm{n}} =\mathrm{C}_{\mathrm{1}} +\mathrm{nC}_{\mathrm{2}} \\ $$$$\mathrm{U}_{\mathrm{0}} =\mathrm{1}\:\Lambda\:\mathrm{U}_{\mathrm{1}} =\mathrm{4} \\ $$$$\Rightarrow\mathrm{U}_{\mathrm{n}} =\mathrm{1}+\mathrm{3n} \\ $$
