
Question Number 134461 by pticantor last updated on 04/Mar/21
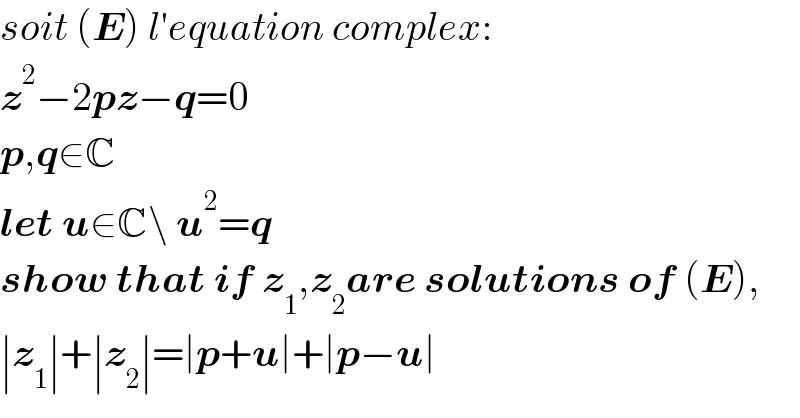
$${soit}\:\left(\boldsymbol{{E}}\right)\:{l}'{equation}\:{complex}: \\ $$$$\boldsymbol{{z}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{pz}}−\boldsymbol{{q}}=\mathrm{0} \\ $$$$\boldsymbol{{p}},\boldsymbol{{q}}\in\mathbb{C} \\ $$$$\boldsymbol{{let}}\:\boldsymbol{{u}}\in\mathbb{C}\backslash\:\boldsymbol{{u}}^{\mathrm{2}} =\boldsymbol{{q}} \\ $$$$\boldsymbol{{show}}\:\boldsymbol{{that}}\:\boldsymbol{{if}}\:\boldsymbol{{z}}_{\mathrm{1}} ,\boldsymbol{{z}}_{\mathrm{2}} \boldsymbol{{are}}\:\boldsymbol{{solutions}}\:\boldsymbol{{of}}\:\left(\boldsymbol{{E}}\right), \\ $$$$\mid\boldsymbol{{z}}_{\mathrm{1}} \mid+\mid\boldsymbol{{z}}_{\mathrm{2}} \mid=\mid\boldsymbol{{p}}+\boldsymbol{{u}}\mid+\mid\boldsymbol{{p}}−\boldsymbol{{u}}\mid \\ $$
