
Question Number 88555 by M±th+et£s last updated on 11/Apr/20

$${slove}\: \\ $$ $$\lceil\frac{{x}}{{a}}\rceil<{a}\:\:\: \\ $$ $${when}\:{a}>\mathrm{1} \\ $$ $$\lceil...\rceil\:{is}\:{ceil}\:{function} \\ $$
Answered by mr W last updated on 11/Apr/20
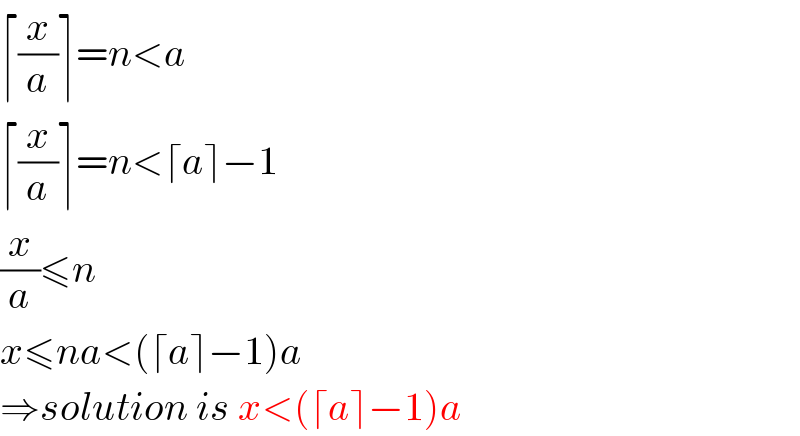
$$\lceil\frac{{x}}{{a}}\rceil={n}<{a} \\ $$ $$\lceil\frac{{x}}{{a}}\rceil={n}<\lceil{a}\rceil−\mathrm{1} \\ $$ $$\frac{{x}}{{a}}\leqslant{n} \\ $$ $${x}\leqslant{na}<\left(\lceil{a}\rceil−\mathrm{1}\right){a} \\ $$ $$\Rightarrow{solution}\:{is}\:{x}<\left(\lceil{a}\rceil−\mathrm{1}\right){a} \\ $$
Commented byM±th+et£s last updated on 11/Apr/20

$${god}\:{bless}\:{you}\:{sir} \\ $$
