Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 49187 by Rahul kharade last updated on 04/Dec/18

∫((sinx)/(sin4x))dx

$$\int\frac{{sinx}}{{sin}\mathrm{4}{x}}{dx} \\ $$$$ \\ $$

Answered by MJS last updated on 04/Dec/18

∫((sin x)/(sin 4x))dx= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =−(1/2)∫(((t^2 +1)^2 )/((t−1)(t+1)(t−1−(√2))(t−1+(√2))(t+1−(√2))(t+1+(√2))))dt= =−(1/2)∫(−(1/(2(t−1)))+(1/(2(t+1)))+((√2)/(4(t−1−(√2))))−((√2)/(4(t−1+(√2))))+((√2)/(4(t+1−(√2))))−((√2)/(4(t+1+(√2)))))= [now solve with formula ∫(dt/(t+a))=ln ∣t+a∣] =((√2)/8)ln ∣((t^2 +2(√2)t+1)/(t^2 −2(√2)t+1))∣ +(1/4)ln ∣((t−1)/(t+1))∣ = =((√2)/8)ln ∣((1+(√2)sin x)/(1−(√2)sin x))∣ +(1/4)ln ∣(1/(tan ((x/2)+(π/4))))∣ +C

$$\int\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:\mathrm{4}{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)\left({t}−\mathrm{1}−\sqrt{\mathrm{2}}\right)\left({t}−\mathrm{1}+\sqrt{\mathrm{2}}\right)\left({t}+\mathrm{1}−\sqrt{\mathrm{2}}\right)\left({t}+\mathrm{1}+\sqrt{\mathrm{2}}\right)}{dt}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\left(−\frac{\mathrm{1}}{\mathrm{2}\left({t}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)}+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}\left({t}−\mathrm{1}−\sqrt{\mathrm{2}}\right)}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}\left({t}−\mathrm{1}+\sqrt{\mathrm{2}}\right)}+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}\left({t}+\mathrm{1}−\sqrt{\mathrm{2}}\right)}−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}\left({t}+\mathrm{1}+\sqrt{\mathrm{2}}\right)}\right)= \\ $$$$\:\:\:\:\:\left[\mathrm{now}\:\mathrm{solve}\:\mathrm{with}\:\mathrm{formula}\:\int\frac{{dt}}{{t}+{a}}=\mathrm{ln}\:\mid{t}+{a}\mid\right] \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\mathrm{ln}\:\mid\frac{{t}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{2}}{t}+\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}{t}+\mathrm{1}}\mid\:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid\:= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\mathrm{ln}\:\mid\frac{\mathrm{1}+\sqrt{\mathrm{2}}\mathrm{sin}\:{x}}{\mathrm{1}−\sqrt{\mathrm{2}}\mathrm{sin}\:{x}}\mid\:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\mid\frac{\mathrm{1}}{\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)}\mid\:+{C} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 04/Dec/18

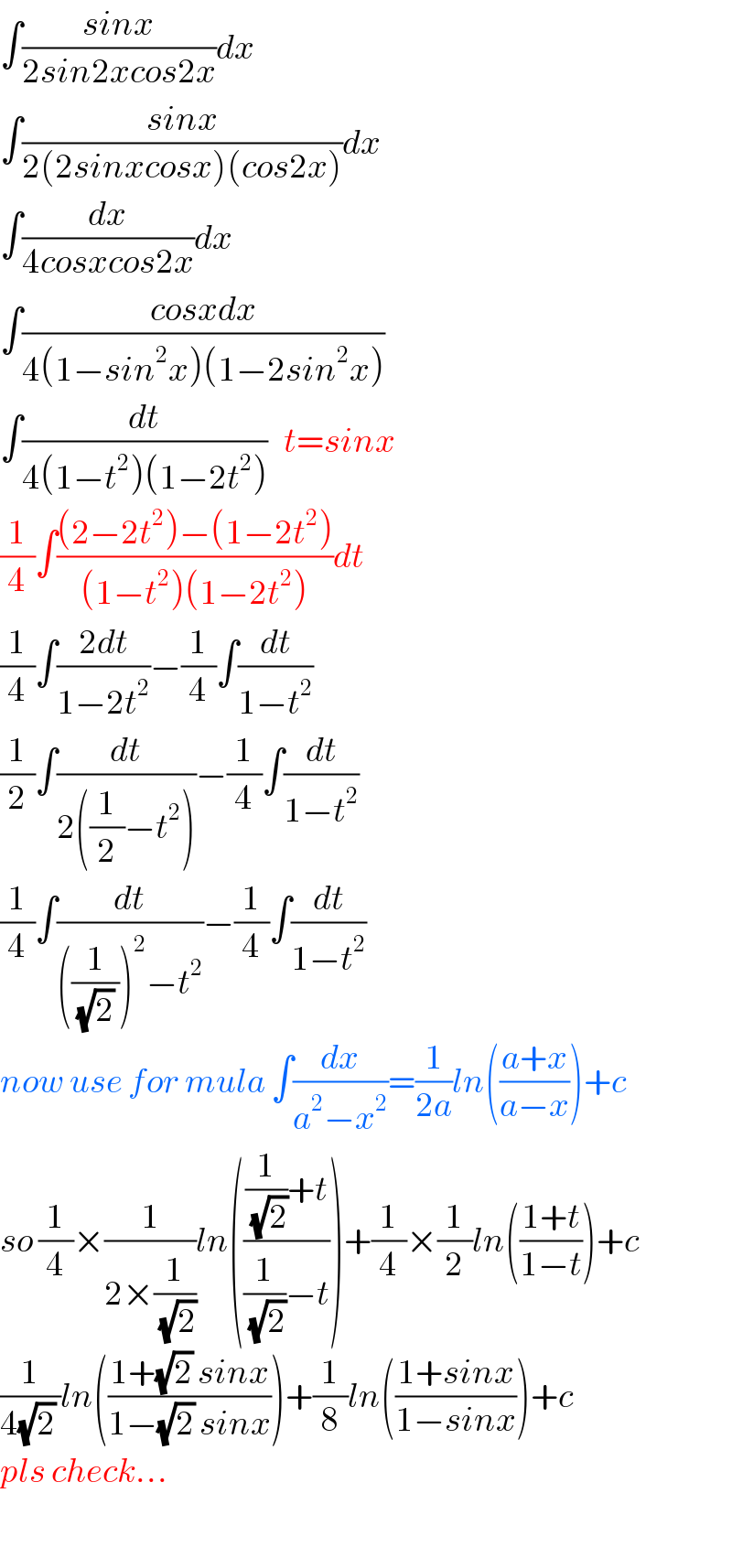
∫((sinx)/(2sin2xcos2x))dx ∫((sinx)/(2(2sinxcosx)(cos2x)))dx ∫(dx/(4cosxcos2x))dx ∫((cosxdx)/(4(1−sin^2 x)(1−2sin^2 x))) ∫(dt/(4(1−t^2 )(1−2t^2 ))) t=sinx (1/4)∫(((2−2t^2 )−(1−2t^2 ))/((1−t^2 )(1−2t^2 )))dt (1/4)∫((2dt)/(1−2t^2 ))−(1/4)∫(dt/(1−t^2 )) (1/2)∫(dt/(2((1/2)−t^2 )))−(1/4)∫(dt/(1−t^2 )) (1/4)∫(dt/(((1/((√2) )))^2 −t^2 ))−(1/4)∫(dt/(1−t^2 )) now use for mula ∫(dx/(a^2 −x^2 ))=(1/(2a))ln(((a+x)/(a−x)))+c so (1/4)×(1/(2×(1/(√2))))ln((((1/(√2))+t)/((1/(√2))−t)))+(1/4)×(1/2)ln(((1+t)/(1−t)))+c (1/(4(√2) ))ln(((1+(√2) sinx)/(1−(√2) sinx)))+(1/8)ln(((1+sinx)/(1−sinx)))+c pls check...

$$\int\frac{{sinx}}{\mathrm{2}{sin}\mathrm{2}{xcos}\mathrm{2}{x}}{dx} \\ $$$$\int\frac{{sinx}}{\mathrm{2}\left(\mathrm{2}{sinxcosx}\right)\left({cos}\mathrm{2}{x}\right)}{dx} \\ $$$$\int\frac{{dx}}{\mathrm{4}{cosxcos}\mathrm{2}{x}}{dx} \\ $$$$\int\frac{{cosxdx}}{\mathrm{4}\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right)\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {x}\right)} \\ $$$$\int\frac{{dt}}{\mathrm{4}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{2}{t}^{\mathrm{2}} \right)}\:\:\:{t}={sinx} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\left(\mathrm{2}−\mathrm{2}{t}^{\mathrm{2}} \right)−\left(\mathrm{1}−\mathrm{2}{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{2}{t}^{\mathrm{2}} \right)}{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{2}{dt}}{\mathrm{1}−\mathrm{2}{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}−{t}^{\mathrm{2}} \right)}−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dt}}{\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}\:}\right)^{\mathrm{2}} −{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$${now}\:{use}\:{for}\:{mula}\:\int\frac{{dx}}{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}{a}}{ln}\left(\frac{{a}+{x}}{{a}−{x}}\right)+{c} \\ $$$${so}\:\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{1}}{\mathrm{2}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}}{ln}\left(\frac{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}+{t}}{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}−{t}}\right)+\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\right)+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}\:}{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{2}}\:{sinx}}{\mathrm{1}−\sqrt{\mathrm{2}}\:{sinx}}\right)+\frac{\mathrm{1}}{\mathrm{8}}{ln}\left(\frac{\mathrm{1}+{sinx}}{\mathrm{1}−{sinx}}\right)+{c} \\ $$$${pls}\:{check}... \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com