
Question Number 169253 by Mastermind last updated on 27/Apr/22

$$\int\frac{−{sinx}}{{e}^{{x}} }{dx} \\ $$$$ \\ $$$${Mastermind} \\ $$
Answered by thfchristopher last updated on 27/Apr/22
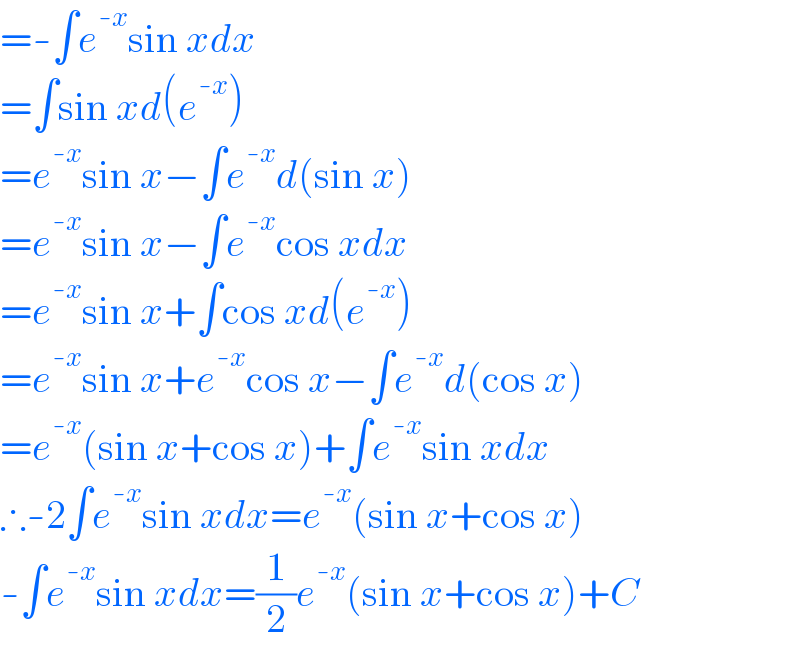
$$=-\int{e}^{-{x}} \mathrm{sin}\:{xdx} \\ $$$$=\int\mathrm{sin}\:{xd}\left({e}^{-{x}} \right) \\ $$$$={e}^{-{x}} \mathrm{sin}\:{x}−\int{e}^{-{x}} {d}\left(\mathrm{sin}\:{x}\right) \\ $$$$={e}^{-{x}} \mathrm{sin}\:{x}−\int{e}^{-{x}} \mathrm{cos}\:{xdx} \\ $$$$={e}^{-{x}} \mathrm{sin}\:{x}+\int\mathrm{cos}\:{xd}\left({e}^{-{x}} \right) \\ $$$$={e}^{-{x}} \mathrm{sin}\:{x}+{e}^{-{x}} \mathrm{cos}\:{x}−\int{e}^{-{x}} {d}\left(\mathrm{cos}\:{x}\right) \\ $$$$={e}^{-{x}} \left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)+\int{e}^{-{x}} \mathrm{sin}\:{xdx} \\ $$$$\therefore-\mathrm{2}\int{e}^{-{x}} \mathrm{sin}\:{xdx}={e}^{-{x}} \left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right) \\ $$$$-\int{e}^{-{x}} \mathrm{sin}\:{xdx}=\frac{\mathrm{1}}{\mathrm{2}}{e}^{-{x}} \left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)+{C} \\ $$
Commented by Mastermind last updated on 28/Apr/22
$${Thanks}\:{sir},\:{i}\:{really}\:{do}\:{appreciate} \\ $$
