
Question Number 129759 by mohammad17 last updated on 18/Jan/21
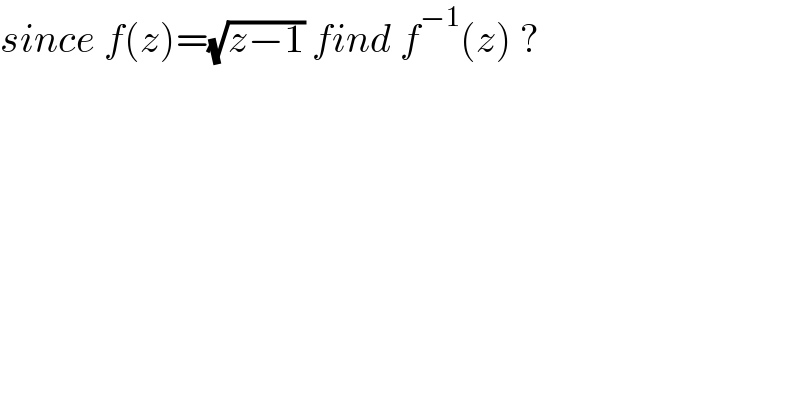
$${since}\:{f}\left({z}\right)=\sqrt{{z}−\mathrm{1}}\:{find}\:{f}^{−\mathrm{1}} \left({z}\right)\:? \\ $$
Answered by I want to learn more last updated on 18/Jan/21
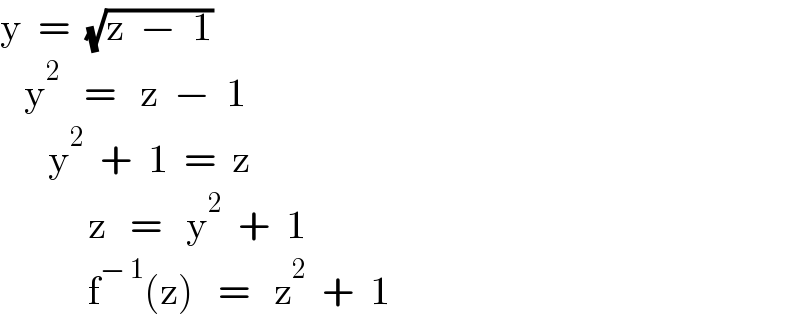
$$\mathrm{y}\:\:=\:\:\sqrt{\mathrm{z}\:\:−\:\:\mathrm{1}} \\ $$$$\:\:\:\mathrm{y}^{\mathrm{2}} \:\:\:=\:\:\:\mathrm{z}\:\:−\:\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\mathrm{y}^{\mathrm{2}} \:\:+\:\:\mathrm{1}\:\:=\:\:\mathrm{z} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{z}\:\:\:=\:\:\:\mathrm{y}^{\mathrm{2}} \:\:+\:\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{f}^{−\:\mathrm{1}} \left(\mathrm{z}\right)\:\:\:=\:\:\:\mathrm{z}^{\mathrm{2}} \:\:+\:\:\mathrm{1} \\ $$
Commented by Olaf last updated on 18/Jan/21
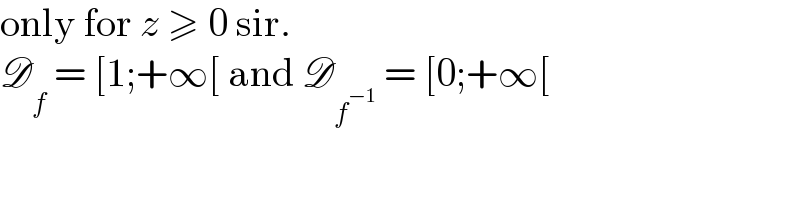
$$\mathrm{only}\:\mathrm{for}\:{z}\:\geqslant\:\mathrm{0}\:\mathrm{sir}. \\ $$$$\mathscr{D}_{{f}} \:=\:\left[\mathrm{1};+\infty\left[\:\mathrm{and}\:\mathscr{D}_{{f}^{−\mathrm{1}} } \:=\:\left[\mathrm{0};+\infty\left[\right.\right.\right.\right. \\ $$
