Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 47566 by tanmay.chaudhury50@gmail.com last updated on 11/Nov/18

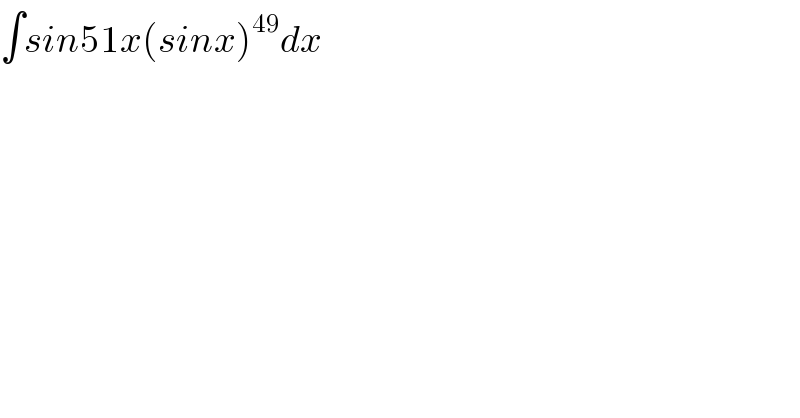
∫sin51x(sinx)^(49) dx

$$\int{sin}\mathrm{51}{x}\left({sinx}\right)^{\mathrm{49}} {dx} \\ $$

Answered by Smail last updated on 12/Nov/18

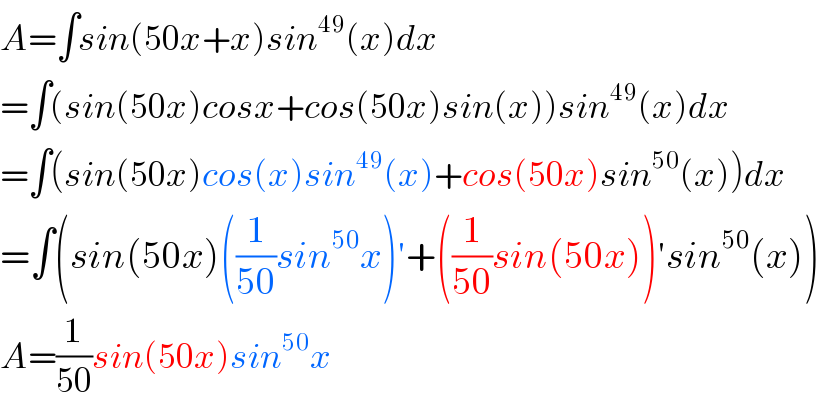
A=∫sin(50x+x)sin^(49) (x)dx =∫(sin(50x)cosx+cos(50x)sin(x))sin^(49) (x)dx =∫(sin(50x)cos(x)sin^(49) (x)+cos(50x)sin^(50) (x))dx =∫(sin(50x)((1/(50))sin^(50) x)′+((1/(50))sin(50x))′sin^(50) (x)) A=(1/(50))sin(50x)sin^(50) x

$${A}=\int{sin}\left(\mathrm{50}{x}+{x}\right){sin}^{\mathrm{49}} \left({x}\right){dx} \\ $$$$=\int\left({sin}\left(\mathrm{50}{x}\right){cosx}+{cos}\left(\mathrm{50}{x}\right){sin}\left({x}\right)\right){sin}^{\mathrm{49}} \left({x}\right){dx} \\ $$$$=\int\left({sin}\left(\mathrm{50}{x}\right){cos}\left({x}\right){sin}^{\mathrm{49}} \left({x}\right)+{cos}\left(\mathrm{50}{x}\right){sin}^{\mathrm{50}} \left({x}\right)\right){dx} \\ $$$$=\int\left({sin}\left(\mathrm{50}{x}\right)\left(\frac{\mathrm{1}}{\mathrm{50}}{sin}^{\mathrm{50}} {x}\right)'+\left(\frac{\mathrm{1}}{\mathrm{50}}{sin}\left(\mathrm{50}{x}\right)\right)'{sin}^{\mathrm{50}} \left({x}\right)\right) \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{50}}{sin}\left(\mathrm{50}{x}\right){sin}^{\mathrm{50}} {x} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 12/Nov/18

∫sin(50+1)x(sinx)^(49) dx ∫[sin50xcosx+cos50xsinx](sinx)^(49) dx ∫sin50xcosx(sinx)^(49) +cos50x(sinx)^(50) dx (1/(50))∫sin50x×50cosx(sinx)^(49) +50cos50x(sinx)^(50) dx (1/(50))∫[sin50x×(d/dx){(sinx)^(50) }+(sinx)^(50) ×(d/dx)(sin50x)]dx (1/(50))∫(d/dx){sin50x×(sinx)^(50) }dx (1/(50))×{sin50x×(sinx)^(50) }+c

$$\int{sin}\left(\mathrm{50}+\mathrm{1}\right){x}\left({sinx}\right)^{\mathrm{49}} {dx} \\ $$$$\int\left[{sin}\mathrm{50}{xcosx}+{cos}\mathrm{50}{xsinx}\right]\left({sinx}\right)^{\mathrm{49}} {dx} \\ $$$$\int{sin}\mathrm{50}{xcosx}\left({sinx}\right)^{\mathrm{49}} +{cos}\mathrm{50}{x}\left({sinx}\right)^{\mathrm{50}} {dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{50}}\int{sin}\mathrm{50}{x}×\mathrm{50}{cosx}\left({sinx}\right)^{\mathrm{49}} +\mathrm{50}{cos}\mathrm{50}{x}\left({sinx}\right)^{\mathrm{50}} {dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{50}}\int\left[{sin}\mathrm{50}{x}×\frac{{d}}{{dx}}\left\{\left({sinx}\right)^{\mathrm{50}} \right\}+\left({sinx}\right)^{\mathrm{50}} ×\frac{{d}}{{dx}}\left({sin}\mathrm{50}{x}\right)\right]{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{50}}\int\frac{{d}}{{dx}}\left\{{sin}\mathrm{50}{x}×\left({sinx}\right)^{\mathrm{50}} \right\}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{50}}×\left\{{sin}\mathrm{50}{x}×\left({sinx}\right)^{\mathrm{50}} \right\}+{c} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com