
Previous in Differential Equation Next in Differential Equation
Question Number 118442 by bramlexs22 last updated on 17/Oct/20
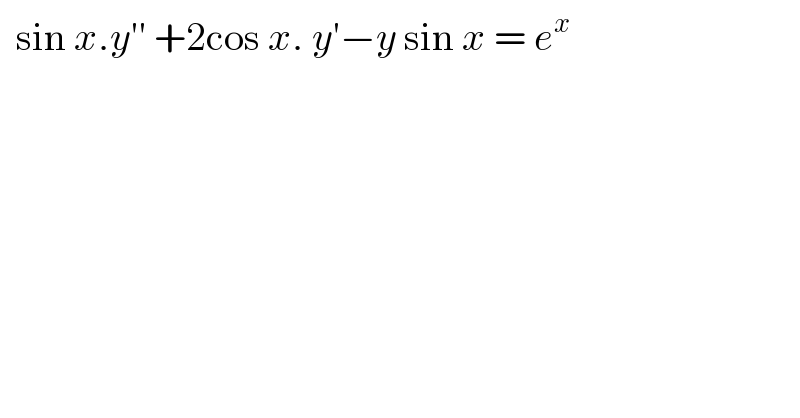
$$\:\:\mathrm{sin}\:{x}.{y}''\:+\mathrm{2cos}\:{x}.\:{y}'−{y}\:\mathrm{sin}\:{x}\:=\:{e}^{{x}} \\ $$$$ \\ $$
Answered by john santu last updated on 17/Oct/20

$$\:{To}\:{solve}\:{it},\:{we}\:{write}\:{it}\:{first}\:{as}\: \\ $$$$\left(\mathrm{sin}\:{x}.{y}''+\mathrm{cos}\:{x}.{y}'\:\right)+\:\left(\mathrm{cos}\:{x}.{y}'\:−\mathrm{sin}\:{x}\right)=\:{e}^{{x}} \\ $$$${by}\:{the}\:{product}\:{rule}\:,\:{the}\:{first}\:{two} \\ $$$${term}\:{in}\:{parentheses}\:{are}\:{the}\:{derivative} \\ $$$${of}\:\mathrm{sin}\:{x}.{y}'\:,\:{while}\:{the}\:{second}\:{two}\: \\ $$$${are}\:{the}\:{derivative}\:{of}\:\mathrm{cos}\:{x}.{y}\:.\:{Then} \\ $$$${the}\:{equation}\:{can}\:{be}\:{written}\:{as} \\ $$$$\frac{{d}}{{dx}\:}\left(\:\mathrm{sin}\:{x}.{y}'+\:\mathrm{cos}\:{x}.{y}\:\right)\:=\:{e}^{{x}} \: \\ $$$$\Rightarrow\:\mathrm{sin}\:{x}.\:{y}'\:+\:\mathrm{cos}\:{x}.{y}\:=\:{e}^{{x}} \:+\:{C}_{\mathrm{1}} \\ $$$$\Rightarrow\frac{{d}}{{dx}}\:\left(\mathrm{sin}\:{x}.{y}\:\right)\:=\:{e}^{{x}} \:+\:{C}_{\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{sin}\:{x}.\:{y}\:=\:{e}^{{x}} \:+\:{C}_{\mathrm{1}} {x}\:+\:{C}_{\mathrm{2}} \\ $$$$\Rightarrow\:{y}\:=\:\frac{{e}^{{x}} \:+\:{C}_{\mathrm{1}} {x}\:+\:{C}_{\mathrm{2}} }{\mathrm{sin}\:{x}} \\ $$$$ \\ $$
