
Question Number 5487 by love math last updated on 16/May/16
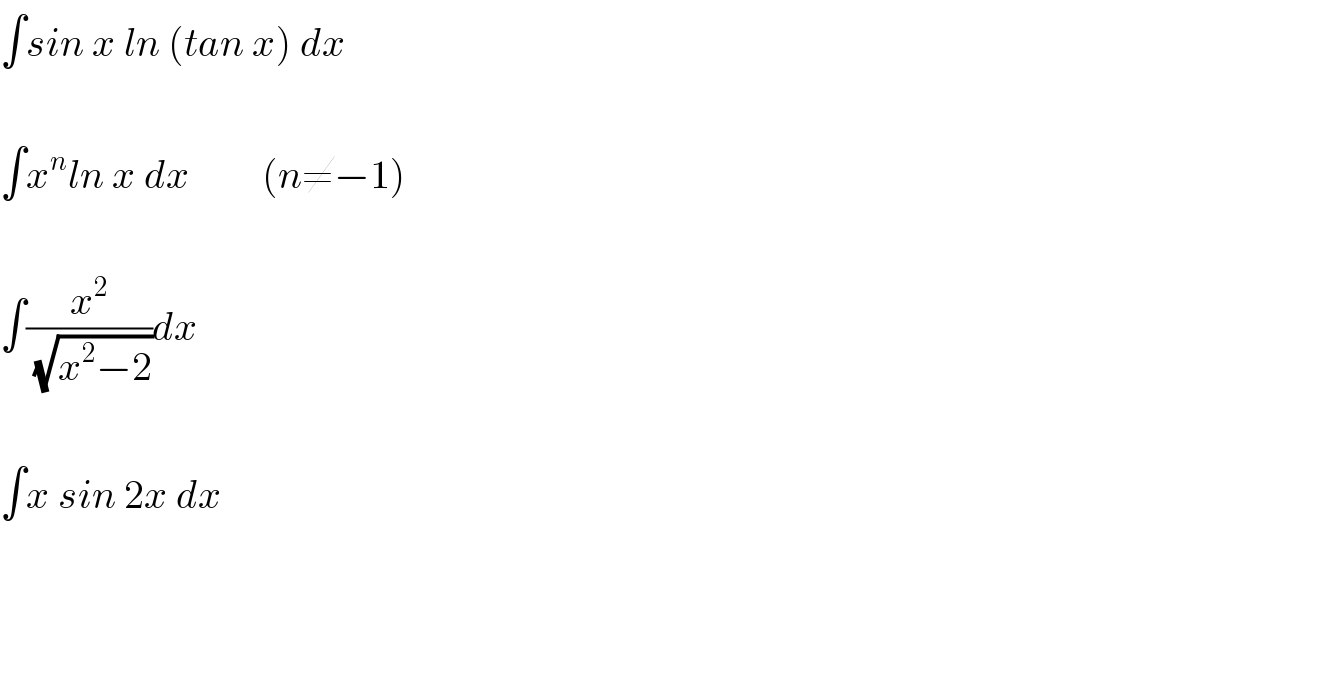
$$\int{sin}\:{x}\:{ln}\:\left({tan}\:{x}\right)\:{dx} \\ $$$$ \\ $$$$\int{x}^{{n}} {ln}\:{x}\:{dx}\:\:\:\:\:\:\:\:\:\left({n}\neq−\mathrm{1}\right) \\ $$$$ \\ $$$$\int\frac{{x}^{\mathrm{2}} }{\sqrt{{x}^{\mathrm{2}} −\mathrm{2}}}{dx} \\ $$$$ \\ $$$$\int{x}\:{sin}\:\mathrm{2}{x}\:{dx} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by nchejane last updated on 16/May/16

$$\mathrm{1}.\int\mathrm{sin}{x}\:{ln}\left({tanx}\right){dx} \\ $$$$=−{cosxln}\left({tanx}\right)\:+\int{cos}\:{x}\:\frac{{sec}\:{x}}{{tan}\:{x}}{dx} \\ $$$$=−{cos}\:{x}\:{ln}\left({tan}\:{x}\right)+\int\frac{{cos}\:{x}}{{sin}\:{x}}{dx} \\ $$$$=−{cos}\:{x}\:{ln}\left({tan}\:{x}\right)+{ln}\left({sin}\:{x}\right)+{c} \\ $$$$ \\ $$$$\mathrm{2}.\int{x}^{{n}} {ln}\:{xdx}=\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}{lnx}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\int{x}^{{n}+\mathrm{1}} \frac{\mathrm{1}}{{x}}{dx} \\ $$$$=\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}{lnx}−\frac{\mathrm{1}}{{n}+\mathrm{1}}×\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}+{k}\:\left({n}\neq−\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{3}.\int\frac{{x}^{\mathrm{2}} }{\sqrt{{x}^{\mathrm{2}} −\mathrm{2}}}{dx}=\sqrt{\mathrm{2}}\int{sec}^{\mathrm{3}} {u}\:{tanu}\frac{\mathrm{1}}{\sqrt{\mathrm{2}\left({sec}^{\mathrm{2}} {u}−\mathrm{1}\right)}}{du}\:\left({let}\:{x}={sec}\:{u}=>{dx}={sec}\:{u}\:{tan}\:{u}\:{du}\right) \\ $$$$=\int{sec}^{\mathrm{3}} \:{u}\:\:{du}=... \\ $$$$ \\ $$$$ \\ $$$$\mathrm{4}.\int{x}\:{sin}\:\mathrm{2}{xdx}=−\frac{{x}}{\mathrm{2}}{cos}\:\mathrm{2}{x}+\frac{\mathrm{1}}{\mathrm{2}}\int{cos}\:\mathrm{2}{x}\:{dx} \\ $$$$=−\frac{{x}}{\mathrm{2}}{cos}\:\mathrm{2}{x}+\frac{{sin}\:\mathrm{2}{x}}{\mathrm{4}}+{k} \\ $$$$ \\ $$
