
Question Number 197583 by cortano12 last updated on 23/Sep/23

$$\:\:\begin{cases}{\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\left(\mathrm{x}+\mathrm{y}\right)}\:=\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\\{\frac{\mathrm{cos}\:\mathrm{y}}{\mathrm{cos}\:\left(\mathrm{x}+\mathrm{y}\right)}\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\end{cases} \\ $$$$\:\:\:\mathrm{find}\:\mathrm{the}\:\mathrm{solution}\: \\ $$
Answered by Sutrisno last updated on 23/Sep/23
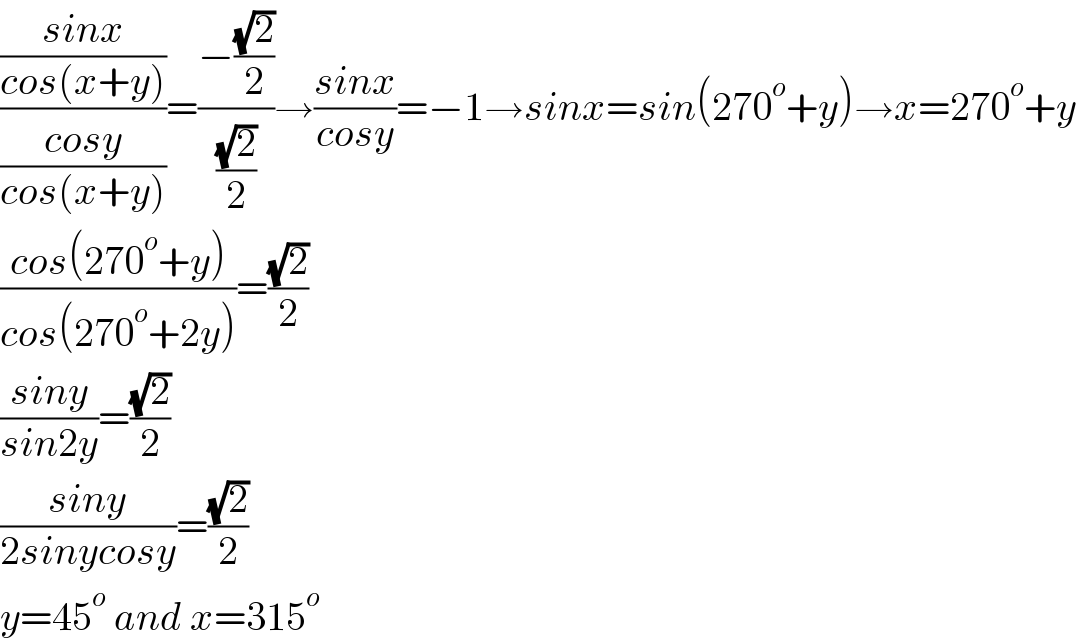
$$\frac{\frac{{sinx}}{{cos}\left({x}+{y}\right)}}{\frac{{cosy}}{{cos}\left({x}+{y}\right)}}=\frac{−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\rightarrow\frac{{sinx}}{{cosy}}=−\mathrm{1}\rightarrow{sinx}={sin}\left(\mathrm{270}^{{o}} +{y}\right)\rightarrow{x}=\mathrm{270}^{{o}} +{y} \\ $$$$\frac{{cos}\left(\mathrm{270}^{{o}} +{y}\right)}{{cos}\left(\mathrm{270}^{{o}} +\mathrm{2}{y}\right)}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\frac{{siny}}{{sin}\mathrm{2}{y}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\frac{{siny}}{\mathrm{2}{sinycosy}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${y}=\mathrm{45}^{{o}} \:{and}\:{x}=\mathrm{315}^{{o}} \\ $$
Commented by mr W last updated on 24/Sep/23

$${generally}: \\ $$$${x}=−\mathrm{45}°+{k}×\mathrm{180}° \\ $$$${y}=\mathrm{45}°+{m}×\mathrm{360}° \\ $$$${k},{m}\in{Z} \\ $$
