
Question Number 77716 by aliesam last updated on 09/Jan/20
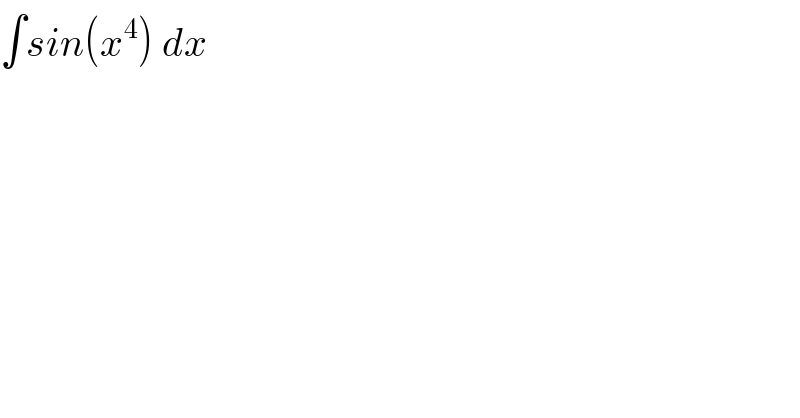
$$\int{sin}\left({x}^{\mathrm{4}} \right)\:{dx} \\ $$
Commented by MJS last updated on 09/Jan/20
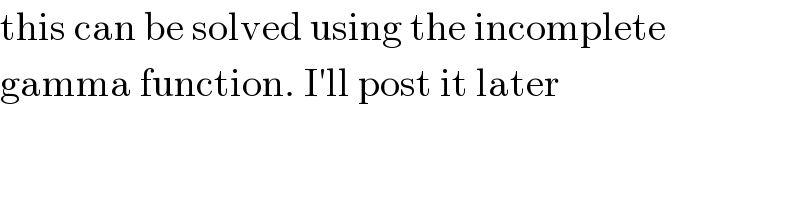
$$\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{using}\:\mathrm{the}\:\mathrm{incomplete} \\ $$$$\mathrm{gamma}\:\mathrm{function}.\:\mathrm{I}'\mathrm{ll}\:\mathrm{post}\:\mathrm{it}\:\mathrm{later} \\ $$
Commented by aliesam last updated on 09/Jan/20

$${thanks}\:{sir} \\ $$
Answered by MJS last updated on 09/Jan/20
![∫sin x^4 dx=−(i/2)∫(e^(ix^4 ) −e^(−ix^4 ) )dx= [t=x((−i))^(1/4) =(x/2)((√(2+(√2)))−i(√(2−(√2)))) → dx=(dt/2)((√(2+(√2)))+i(√(2−(√2))))] =(1/4)((√(2−(√2)))−i(√(2+(√2))))∫(e^(−t^4 ) +e^t^4 )dt ∫e^(−t^4 ) dt=−((√2)/8)(1−i)Γ ((1/4), −t^4 ) ∫e^t^4 dt=−(1/4)Γ ((1/4), t^4 ) ...](Q77748.png)
$$\int\mathrm{sin}\:{x}^{\mathrm{4}} \:{dx}=−\frac{\mathrm{i}}{\mathrm{2}}\int\left(\mathrm{e}^{\mathrm{i}{x}^{\mathrm{4}} } −\mathrm{e}^{−\mathrm{i}{x}^{\mathrm{4}} } \right){dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}\sqrt[{\mathrm{4}}]{−\mathrm{i}}\:=\frac{{x}}{\mathrm{2}}\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}−\mathrm{i}\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}\right)\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{2}}\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}+\mathrm{i}\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}−\mathrm{i}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}\right)\int\left(\mathrm{e}^{−{t}^{\mathrm{4}} } +\mathrm{e}^{{t}^{\mathrm{4}} } \right){dt} \\ $$$$\int\mathrm{e}^{−{t}^{\mathrm{4}} } {dt}=−\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\left(\mathrm{1}−\mathrm{i}\right)\Gamma\:\left(\frac{\mathrm{1}}{\mathrm{4}},\:−{t}^{\mathrm{4}} \right) \\ $$$$\int\mathrm{e}^{{t}^{\mathrm{4}} } {dt}=−\frac{\mathrm{1}}{\mathrm{4}}\Gamma\:\left(\frac{\mathrm{1}}{\mathrm{4}},\:{t}^{\mathrm{4}} \right) \\ $$$$... \\ $$
Commented by aliesam last updated on 09/Jan/20
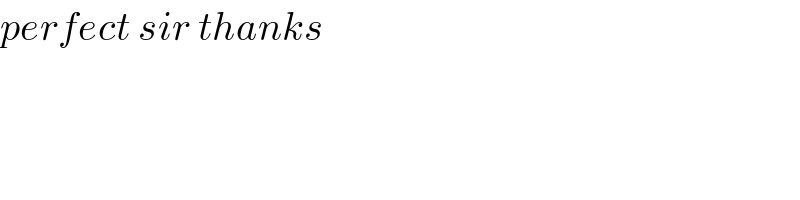
$${perfect}\:{sir}\:{thanks} \\ $$
