Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 161919 by talminator2856791 last updated on 24/Dec/21

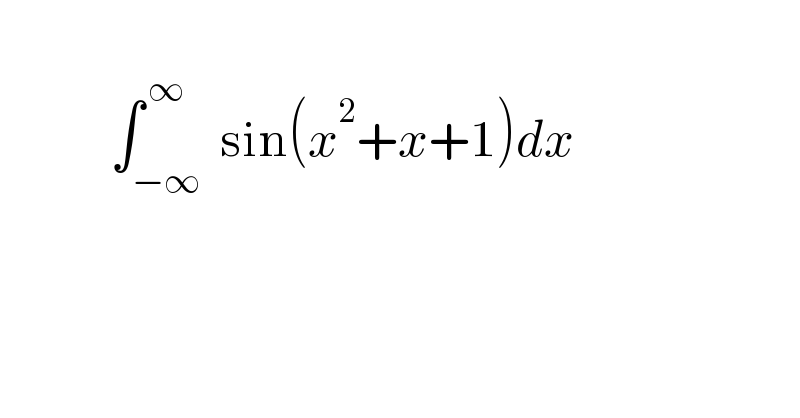
∫_(−∞) ^( ∞) sin(x^2 +x+1)dx

$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\int_{−\infty} ^{\:\infty} \:\mathrm{sin}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right){dx}\: \\ $$$$\: \\ $$

Answered by Lordose last updated on 24/Dec/21

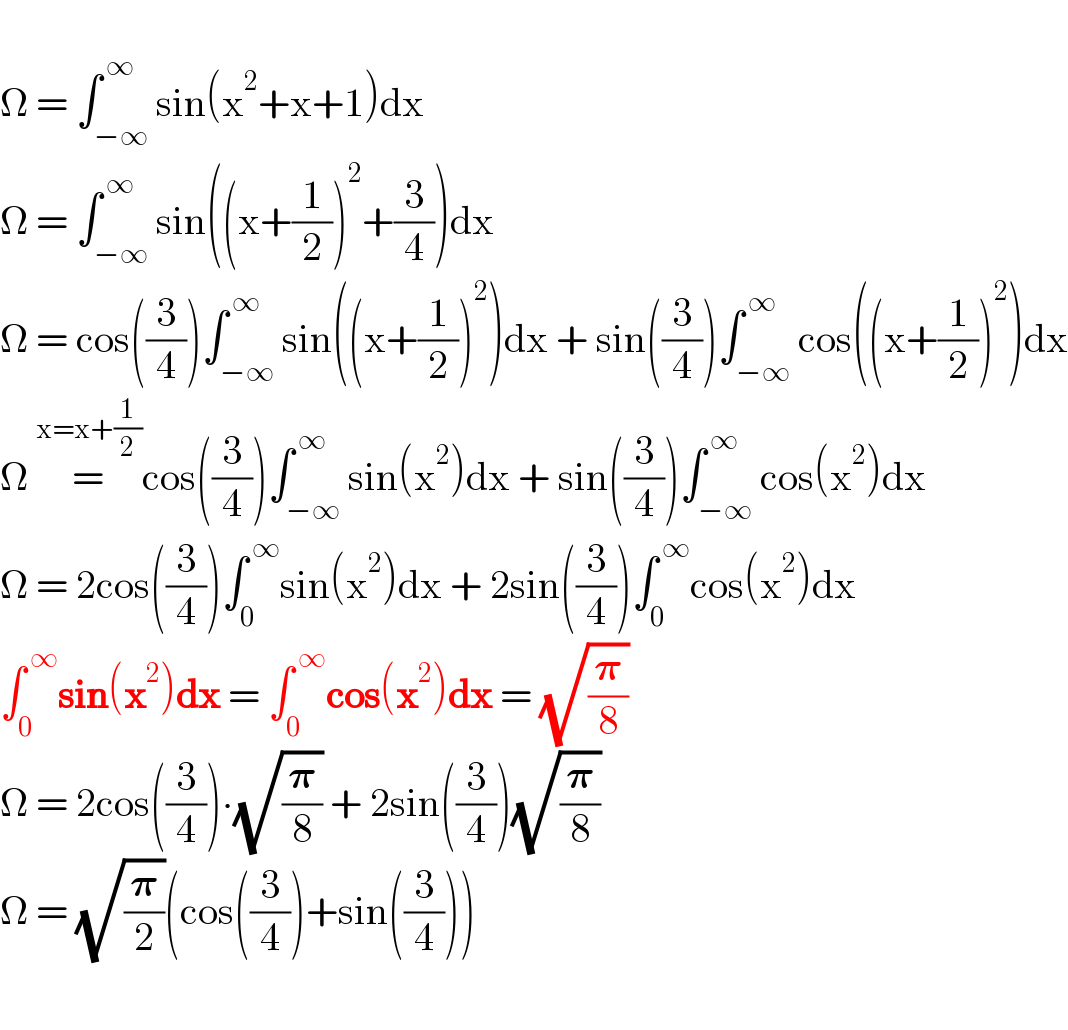
Ω = ∫_(−∞) ^( ∞) sin(x^2 +x+1)dx Ω = ∫_(−∞) ^( ∞) sin((x+(1/2))^2 +(3/4))dx Ω = cos((3/4))∫_(−∞) ^( ∞) sin((x+(1/2))^2 )dx + sin((3/4))∫_(−∞) ^( ∞) cos((x+(1/2))^2 )dx Ω =^(x=x+(1/2)) cos((3/4))∫_(−∞) ^( ∞) sin(x^2 )dx + sin((3/4))∫_(−∞) ^( ∞) cos(x^2 )dx Ω = 2cos((3/4))∫_0 ^( ∞) sin(x^2 )dx + 2sin((3/4))∫_0 ^( ∞) cos(x^2 )dx ∫_0 ^( ∞) sin(x^2 )dx = ∫_0 ^( ∞) cos(x^2 )dx = (√(𝛑/8)) Ω = 2cos((3/4))∙(√(𝛑/8)) + 2sin((3/4))(√(𝛑/8)) Ω = (√(𝛑/2))(cos((3/4))+sin((3/4)))

$$ \\ $$$$\Omega\:=\:\int_{−\infty} ^{\:\infty} \mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)\mathrm{dx} \\ $$$$\Omega\:=\:\int_{−\infty} ^{\:\infty} \mathrm{sin}\left(\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\right)\mathrm{dx} \\ $$$$\Omega\:=\:\mathrm{cos}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\int_{−\infty} ^{\:\infty} \mathrm{sin}\left(\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \right)\mathrm{dx}\:+\:\mathrm{sin}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\int_{−\infty} ^{\:\infty} \mathrm{cos}\left(\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$\Omega\:\overset{\mathrm{x}=\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}} {=}\mathrm{cos}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\int_{−\infty} ^{\:\infty} \mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}\:+\:\mathrm{sin}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\int_{−\infty} ^{\:\infty} \mathrm{cos}\left(\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$\Omega\:=\:\mathrm{2cos}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\int_{\mathrm{0}} ^{\:\infty} \mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}\:+\:\mathrm{2sin}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\int_{\mathrm{0}} ^{\:\infty} \mathrm{cos}\left(\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} \right)\boldsymbol{\mathrm{dx}}\:=\:\int_{\mathrm{0}} ^{\:\infty} \boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} \right)\boldsymbol{\mathrm{dx}}\:=\:\sqrt{\frac{\boldsymbol{\pi}}{\mathrm{8}}} \\ $$$$\Omega\:=\:\mathrm{2cos}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\centerdot\sqrt{\frac{\boldsymbol{\pi}}{\mathrm{8}}}\:+\:\mathrm{2sin}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\sqrt{\frac{\boldsymbol{\pi}}{\mathrm{8}}} \\ $$$$\Omega\:=\:\sqrt{\frac{\boldsymbol{\pi}}{\mathrm{2}}}\left(\mathrm{cos}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)+\mathrm{sin}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\right) \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com