
Question Number 193436 by beto last updated on 14/Jun/23
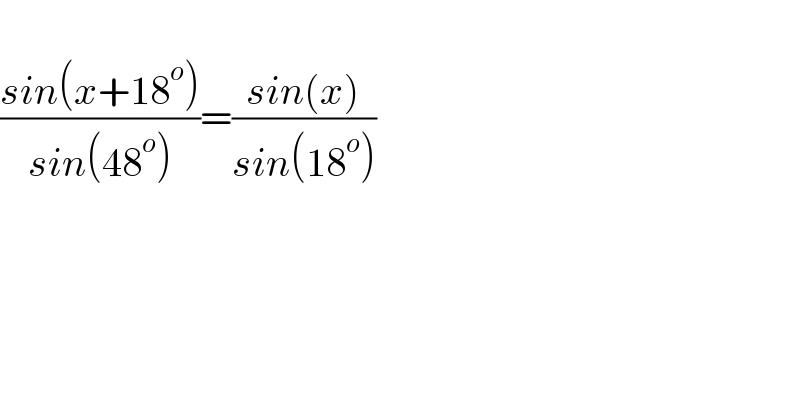
$$ \\ $$$$\frac{{sin}\left({x}+\mathrm{18}^{{o}} \right)}{{sin}\left(\mathrm{48}^{{o}} \right)}=\frac{{sin}\left({x}\right)}{{sin}\left(\mathrm{18}^{{o}} \right)} \\ $$$$ \\ $$
Answered by a.lgnaoui last updated on 14/Jun/23
![sin (x+18)=((sin 48)/(sin 18))sin x sin xcos 18+cos xsin 18=((sin 48)/(sin 18))sin x cos x[tan xcos 18+sin 18]=cos x[((sin 48)/(sin 18))tan x] ⇒tan xcos 18+sin 18=((sin 48)/(sin 18))tan x tan x(((sin 48)/(sin 18))−cos 18)=sin 18 tan x(sin 48−sin 18cos 18)=sin^2 18 ⇒tan x=((sin^2 18 )/(sin 48−sin 18cos 18)) =0,21255656167 x=12](Q193445.png)
$$\mathrm{sin}\:\left(\mathrm{x}+\mathrm{18}\right)=\frac{\mathrm{sin}\:\mathrm{48}}{\mathrm{sin}\:\mathrm{18}}\mathrm{sin}\:\mathrm{x} \\ $$$$\mathrm{sin}\:\mathrm{xcos}\:\mathrm{18}+\mathrm{cos}\:\mathrm{xsin}\:\mathrm{18}=\frac{\mathrm{sin}\:\mathrm{48}}{\mathrm{sin}\:\mathrm{18}}\mathrm{sin}\:\mathrm{x} \\ $$$$\mathrm{cos}\:\mathrm{x}\left[\mathrm{tan}\:\mathrm{xcos}\:\mathrm{18}+\mathrm{sin}\:\mathrm{18}\right]=\mathrm{cos}\:\mathrm{x}\left[\frac{\mathrm{sin}\:\mathrm{48}}{\mathrm{sin}\:\mathrm{18}}\mathrm{tan}\:\mathrm{x}\right] \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{xcos}\:\mathrm{18}+\mathrm{sin}\:\mathrm{18}=\frac{\mathrm{sin}\:\mathrm{48}}{\mathrm{sin}\:\mathrm{18}}\mathrm{tan}\:\mathrm{x} \\ $$$$\mathrm{tan}\:\mathrm{x}\left(\frac{\mathrm{sin}\:\mathrm{48}}{\mathrm{sin}\:\mathrm{18}}−\mathrm{cos}\:\mathrm{18}\right)=\mathrm{sin}\:\mathrm{18} \\ $$$$\mathrm{tan}\:\mathrm{x}\left(\mathrm{sin}\:\mathrm{48}−\mathrm{sin}\:\mathrm{18cos}\:\mathrm{18}\right)=\mathrm{sin}\:^{\mathrm{2}} \mathrm{18} \\ $$$$\Rightarrow\mathrm{tan}\:\boldsymbol{\mathrm{x}}=\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{18}\:}{\mathrm{sin}\:\mathrm{48}−\mathrm{sin}\:\mathrm{18cos}\:\mathrm{18}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{0},\mathrm{21255656167} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}=\mathrm{12} \\ $$$$ \\ $$
