
Question Number 211075 by ajfour last updated on 27/Aug/24
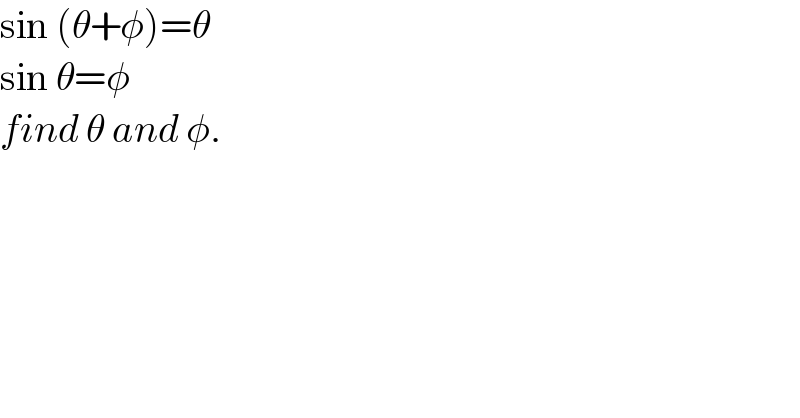
$$\mathrm{sin}\:\left(\theta+\phi\right)=\theta \\ $$$$\mathrm{sin}\:\theta=\phi \\ $$$${find}\:\theta\:{and}\:\phi. \\ $$
Answered by Ghisom last updated on 27/Aug/24

$$\mathrm{we}\:\mathrm{can}\:\mathrm{only}\:\mathrm{approximate} \\ $$$$\phi=\mathrm{sin}\:\theta \\ $$$$\mathrm{sin}\:\left(\theta+\mathrm{sin}\:\theta\right)\:=\theta \\ $$$$\mathrm{1}.\:\theta=\phi=\mathrm{0} \\ $$$$\mathrm{2}.\:\theta\approx\pm.\mathrm{973696169714}\wedge\phi\approx\pm.\mathrm{826969516935} \\ $$
Answered by ajfour last updated on 27/Aug/24
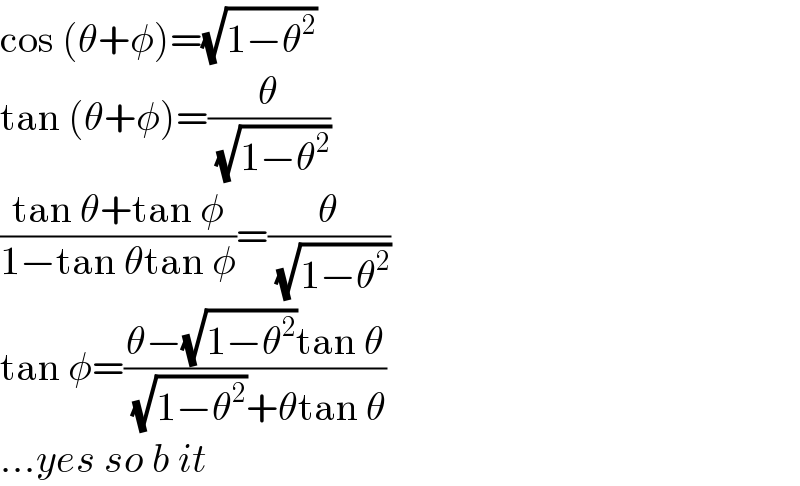
$$\mathrm{cos}\:\left(\theta+\phi\right)=\sqrt{\mathrm{1}−\theta^{\mathrm{2}} } \\ $$$$\mathrm{tan}\:\left(\theta+\phi\right)=\frac{\theta}{\:\sqrt{\mathrm{1}−\theta^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{tan}\:\theta+\mathrm{tan}\:\phi}{\mathrm{1}−\mathrm{tan}\:\theta\mathrm{tan}\:\phi}=\frac{\theta}{\:\sqrt{\mathrm{1}−\theta^{\mathrm{2}} }} \\ $$$$\mathrm{tan}\:\phi=\frac{\theta−\sqrt{\mathrm{1}−\theta^{\mathrm{2}} }\mathrm{tan}\:\theta}{\:\sqrt{\mathrm{1}−\theta^{\mathrm{2}} }+\theta\mathrm{tan}\:\theta} \\ $$$$...{yes}\:{so}\:{b}\:{it} \\ $$
