
Question Number 188475 by cortano12 last updated on 02/Mar/23
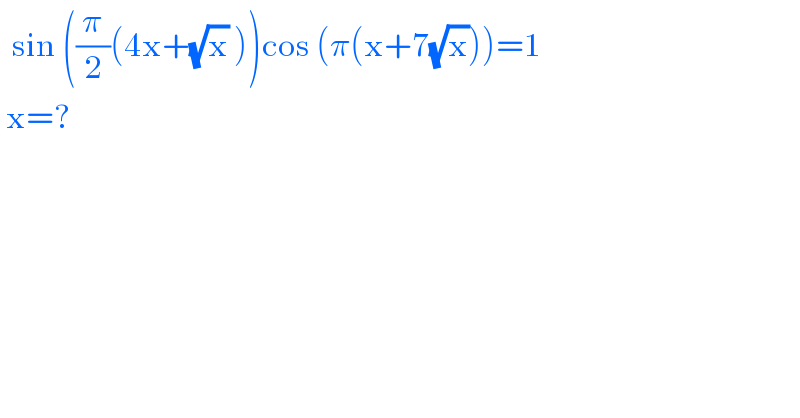
$$\:\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}\left(\mathrm{4x}+\sqrt{\mathrm{x}}\:\right)\right)\mathrm{cos}\:\left(\pi\left(\mathrm{x}+\mathrm{7}\sqrt{\mathrm{x}}\right)\right)=\mathrm{1} \\ $$$$\:\mathrm{x}=? \\ $$
Answered by Frix last updated on 02/Mar/23
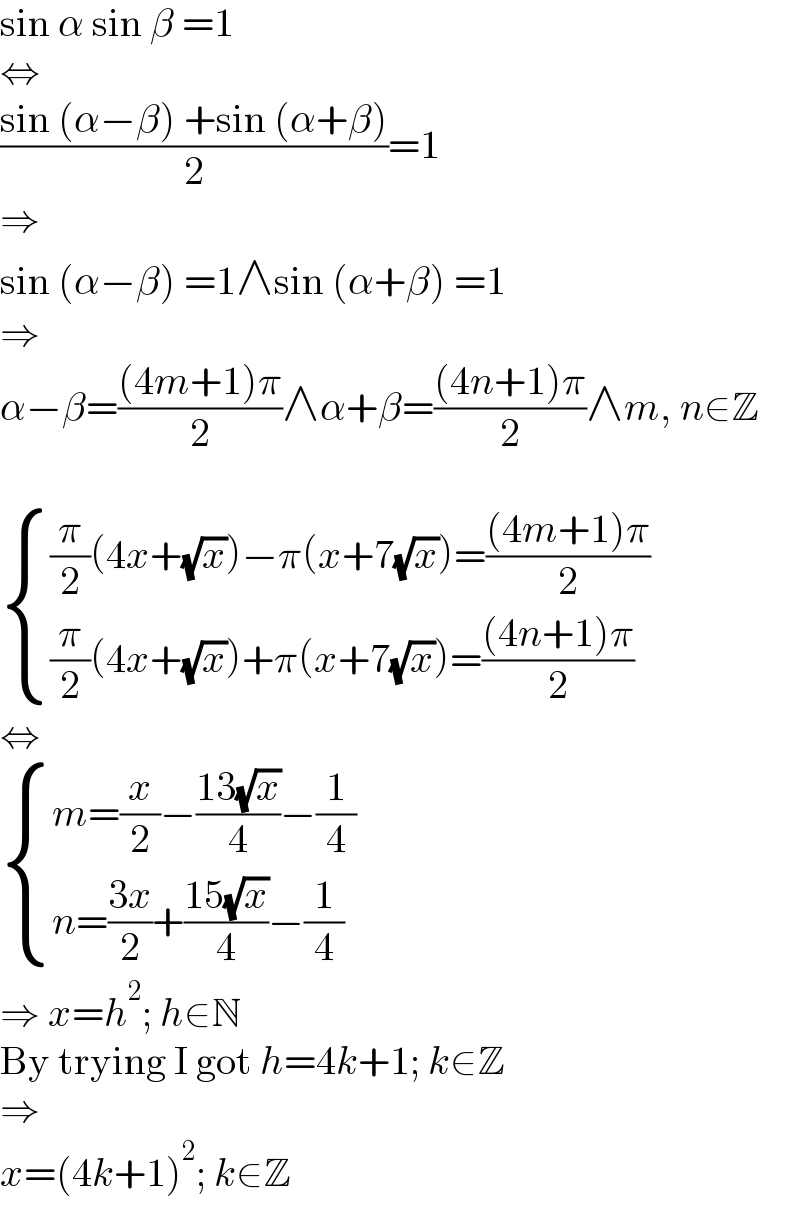
$$\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta\:=\mathrm{1} \\ $$$$\Leftrightarrow \\ $$$$\frac{\mathrm{sin}\:\left(\alpha−\beta\right)\:+\mathrm{sin}\:\left(\alpha+\beta\right)}{\mathrm{2}}=\mathrm{1} \\ $$$$\Rightarrow \\ $$$$\mathrm{sin}\:\left(\alpha−\beta\right)\:=\mathrm{1}\wedge\mathrm{sin}\:\left(\alpha+\beta\right)\:=\mathrm{1} \\ $$$$\Rightarrow \\ $$$$\alpha−\beta=\frac{\left(\mathrm{4}{m}+\mathrm{1}\right)\pi}{\mathrm{2}}\wedge\alpha+\beta=\frac{\left(\mathrm{4}{n}+\mathrm{1}\right)\pi}{\mathrm{2}}\wedge{m},\:{n}\in\mathbb{Z} \\ $$$$ \\ $$$$\begin{cases}{\frac{\pi}{\mathrm{2}}\left(\mathrm{4}{x}+\sqrt{{x}}\right)−\pi\left({x}+\mathrm{7}\sqrt{{x}}\right)=\frac{\left(\mathrm{4}{m}+\mathrm{1}\right)\pi}{\mathrm{2}}}\\{\frac{\pi}{\mathrm{2}}\left(\mathrm{4}{x}+\sqrt{{x}}\right)+\pi\left({x}+\mathrm{7}\sqrt{{x}}\right)=\frac{\left(\mathrm{4}{n}+\mathrm{1}\right)\pi}{\mathrm{2}}}\end{cases} \\ $$$$\Leftrightarrow \\ $$$$\begin{cases}{{m}=\frac{{x}}{\mathrm{2}}−\frac{\mathrm{13}\sqrt{{x}}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}}\\{{n}=\frac{\mathrm{3}{x}}{\mathrm{2}}+\frac{\mathrm{15}\sqrt{{x}}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}}\end{cases} \\ $$$$\Rightarrow\:{x}={h}^{\mathrm{2}} ;\:{h}\in\mathbb{N} \\ $$$$\mathrm{By}\:\mathrm{trying}\:\mathrm{I}\:\mathrm{got}\:{h}=\mathrm{4}{k}+\mathrm{1};\:{k}\in\mathbb{Z} \\ $$$$\Rightarrow \\ $$$${x}=\left(\mathrm{4}{k}+\mathrm{1}\right)^{\mathrm{2}} ;\:{k}\in\mathbb{Z} \\ $$
Commented by cortano12 last updated on 02/Mar/23
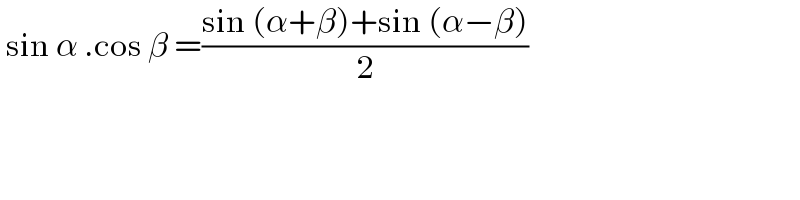
$$\:\mathrm{sin}\:\alpha\:.\mathrm{cos}\:\beta\:=\frac{\mathrm{sin}\:\left(\alpha+\beta\right)+\mathrm{sin}\:\left(\alpha−\beta\right)}{\mathrm{2}} \\ $$
Commented by Frix last updated on 02/Mar/23

$$\mathrm{Yes},\:\mathrm{that}\:\mathrm{is}\:\mathrm{what}\:\mathrm{I}\:\mathrm{used}. \\ $$
