
Question Number 8993 by tawakalitu last updated on 11/Nov/16
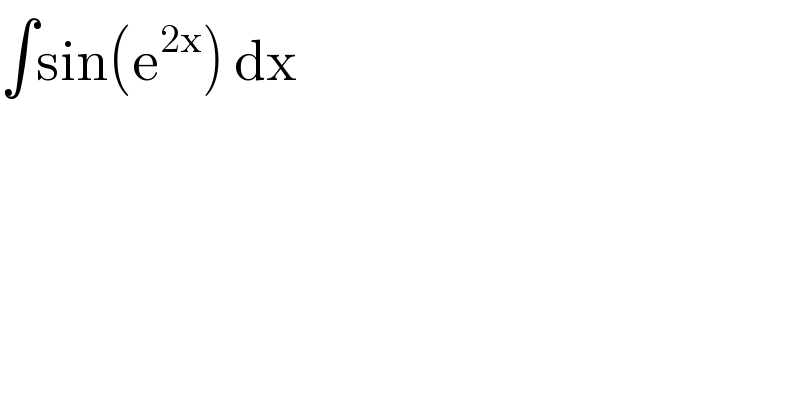
$$\int\mathrm{sin}\left(\mathrm{e}^{\mathrm{2x}} \right)\:\mathrm{dx} \\ $$
Commented by FilupSmith last updated on 12/Nov/16
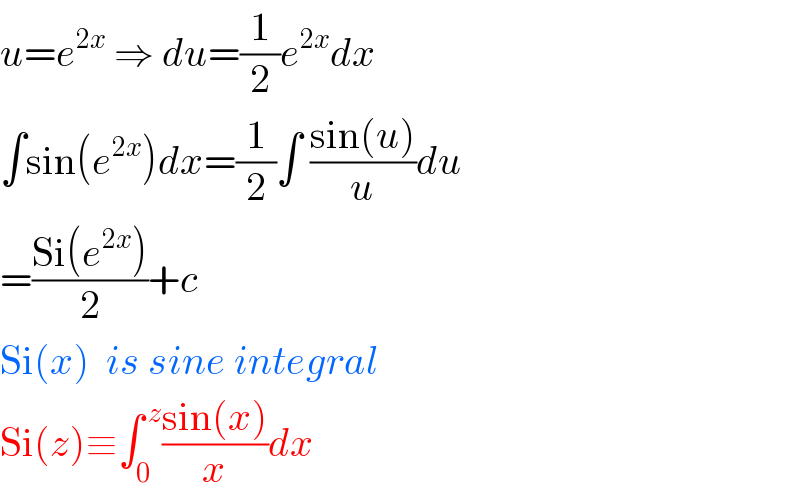
$${u}={e}^{\mathrm{2}{x}} \:\Rightarrow\:{du}=\frac{\mathrm{1}}{\mathrm{2}}{e}^{\mathrm{2}{x}} {dx} \\ $$$$\int\mathrm{sin}\left({e}^{\mathrm{2}{x}} \right){dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{sin}\left({u}\right)}{{u}}{du} \\ $$$$=\frac{\mathrm{Si}\left({e}^{\mathrm{2}{x}} \right)}{\mathrm{2}}+{c} \\ $$$$\mathrm{Si}\left({x}\right)\:\:{is}\:{sine}\:{integral} \\ $$$$\mathrm{Si}\left({z}\right)\equiv\int_{\mathrm{0}} ^{\:{z}} \frac{\mathrm{sin}\left({x}\right)}{{x}}{dx} \\ $$
Commented by tawakalitu last updated on 12/Nov/16

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
