
Question Number 59326 by prattushdas7@gmail.com last updated on 08/May/19
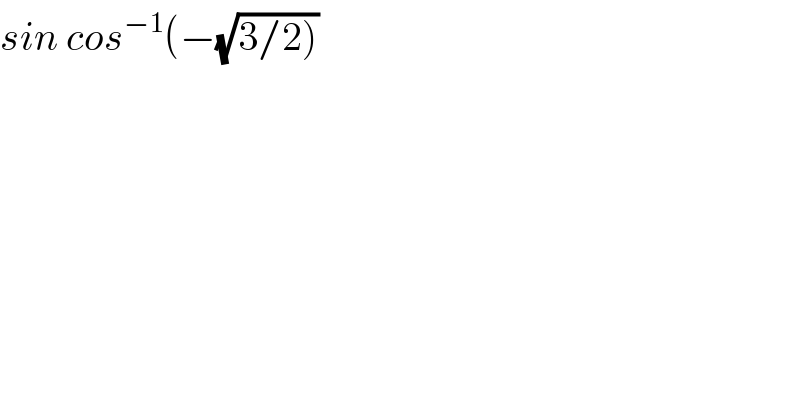
$${sin}\:{cos}^{−\mathrm{1}} \left(−\sqrt{\left.\mathrm{3}/\mathrm{2}\right)}\right. \\ $$
Commented by MJS last updated on 08/May/19
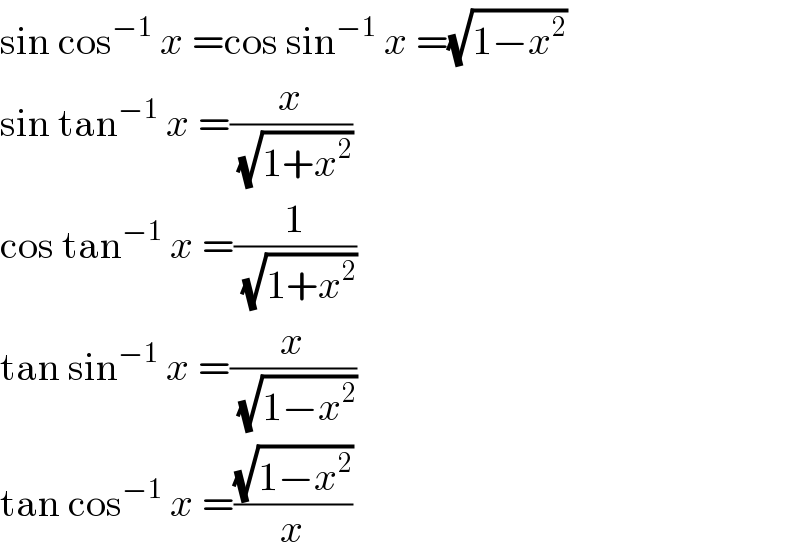
$$\mathrm{sin}\:\mathrm{cos}^{−\mathrm{1}} \:{x}\:=\mathrm{cos}\:\mathrm{sin}^{−\mathrm{1}} \:{x}\:=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\mathrm{sin}\:\mathrm{tan}^{−\mathrm{1}} \:{x}\:=\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$$\mathrm{cos}\:\mathrm{tan}^{−\mathrm{1}} \:{x}\:=\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$$\mathrm{tan}\:\mathrm{sin}^{−\mathrm{1}} \:{x}\:=\frac{{x}}{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\mathrm{tan}\:\mathrm{cos}^{−\mathrm{1}} \:{x}\:=\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}} \\ $$
Answered by tanmay last updated on 08/May/19
![(3/2)=1.5 (√(1.5)) ≈1.22 1≥cosθ≥−1 so question is sincos^(−1) (((−(√3))/2)) =sincos^(−1) (−cos(π/6)) =sincos^(−1) [cos(π−(π/6))] =sin(π−(π/6)) =sin(π/6) =(1/2) or sincos^(−1) (((−(√3))/2)) cosa=((−(√3))/2)→cos^2 a=(3/4) sin^2 a=1−(3/4)=(1/4) sina=(1/2)](Q59327.png)
$$\frac{\mathrm{3}}{\mathrm{2}}=\mathrm{1}.\mathrm{5} \\ $$$$\sqrt{\mathrm{1}.\mathrm{5}}\:\approx\mathrm{1}.\mathrm{22} \\ $$$$\mathrm{1}\geqslant{cos}\theta\geqslant−\mathrm{1} \\ $$$${so}\:{question}\:{is}\: \\ $$$${sincos}^{−\mathrm{1}} \left(\frac{−\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$={sincos}^{−\mathrm{1}} \left(−{cos}\frac{\pi}{\mathrm{6}}\right) \\ $$$$={sincos}^{−\mathrm{1}} \left[{cos}\left(\pi−\frac{\pi}{\mathrm{6}}\right)\right] \\ $$$$={sin}\left(\pi−\frac{\pi}{\mathrm{6}}\right) \\ $$$$={sin}\frac{\pi}{\mathrm{6}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${or}\: \\ $$$${sincos}^{−\mathrm{1}} \left(\frac{−\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$${cosa}=\frac{−\sqrt{\mathrm{3}}}{\mathrm{2}}\rightarrow{cos}^{\mathrm{2}} {a}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${sin}^{\mathrm{2}} {a}=\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${sina}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
