
Question Number 97041 by bemath last updated on 06/Jun/20
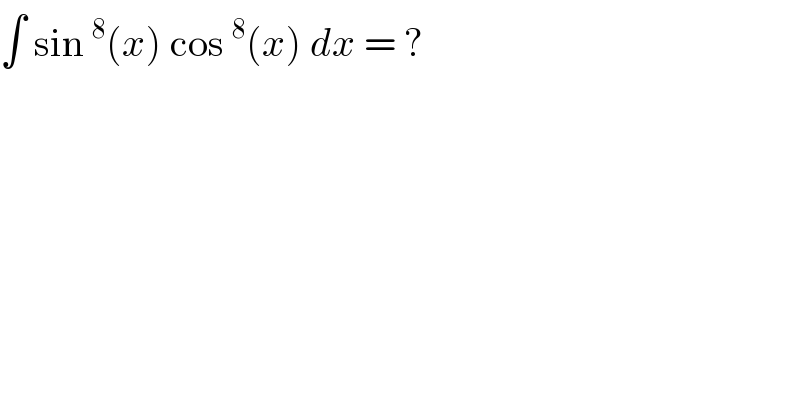
$$\int\:\mathrm{sin}\:^{\mathrm{8}} \left({x}\right)\:\mathrm{cos}\:^{\mathrm{8}} \left({x}\right)\:{dx}\:=\:? \\ $$
Answered by john santu last updated on 06/Jun/20
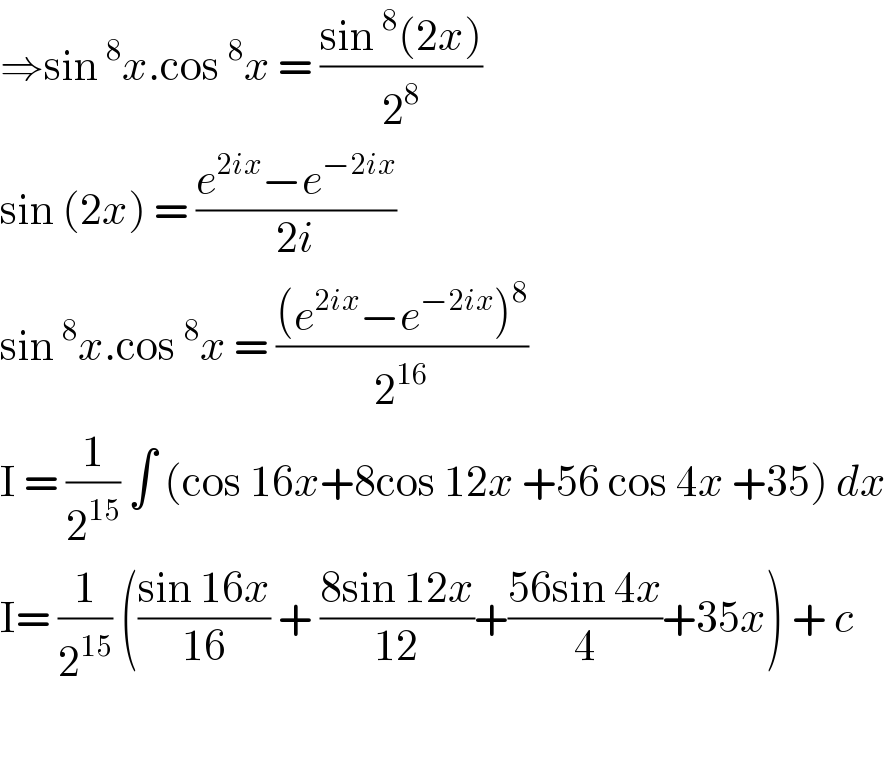
$$\Rightarrow\mathrm{sin}\:^{\mathrm{8}} {x}.\mathrm{cos}\:^{\mathrm{8}} {x}\:=\:\frac{\mathrm{sin}\:^{\mathrm{8}} \left(\mathrm{2}{x}\right)}{\mathrm{2}^{\mathrm{8}} } \\ $$$$\mathrm{sin}\:\left(\mathrm{2}{x}\right)\:=\:\frac{{e}^{\mathrm{2}{ix}} −{e}^{−\mathrm{2}{ix}} }{\mathrm{2}{i}} \\ $$$$\mathrm{sin}\:^{\mathrm{8}} {x}.\mathrm{cos}\:^{\mathrm{8}} {x}\:=\:\frac{\left({e}^{\mathrm{2}{ix}} −{e}^{−\mathrm{2}{ix}} \right)^{\mathrm{8}} }{\mathrm{2}^{\mathrm{16}} } \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{15}} }\:\int\:\left(\mathrm{cos}\:\mathrm{16}{x}+\mathrm{8cos}\:\mathrm{12}{x}\:+\mathrm{56}\:\mathrm{cos}\:\mathrm{4}{x}\:+\mathrm{35}\right)\:{dx} \\ $$$$\mathrm{I}=\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{15}} }\:\left(\frac{\mathrm{sin}\:\mathrm{16}{x}}{\mathrm{16}}\:+\:\frac{\mathrm{8sin}\:\mathrm{12}{x}}{\mathrm{12}}+\frac{\mathrm{56sin}\:\mathrm{4}{x}}{\mathrm{4}}+\mathrm{35}{x}\right)\:+\:{c}\: \\ $$$$ \\ $$
Answered by Sourav mridha last updated on 06/Jun/20
![let sinx=m ∫(1−m^2 )^7 m^8 dm =∫[Σ_(r=0) ^7 C_r ^7 (1)^(7−r) .(−m^2 )^r .].m^8 dm =Σ_(r=0) ^7 (−1)^r C_r ^7 [∫m^(2r+8) dm] =Σ_(r=0) ^7 (−1)^r C_r ^7 (((sin(x))^(2r+9) )/(2r+9)).+k](Q97046.png)
$$\boldsymbol{{let}}\:\boldsymbol{{sinx}}=\boldsymbol{{m}} \\ $$$$\int\left(\mathrm{1}−\boldsymbol{{m}}^{\mathrm{2}} \right)^{\mathrm{7}} \boldsymbol{{m}}^{\mathrm{8}} \boldsymbol{{dm}} \\ $$$$=\int\left[\underset{{r}=\mathrm{0}} {\overset{\mathrm{7}} {\sum}}\overset{\mathrm{7}} {\boldsymbol{{C}}}_{\boldsymbol{{r}}} \left(\mathrm{1}\right)^{\mathrm{7}−\boldsymbol{{r}}} .\left(−\boldsymbol{{m}}^{\mathrm{2}} \right)^{\boldsymbol{{r}}} .\right].\boldsymbol{{m}}^{\mathrm{8}} \boldsymbol{{dm}} \\ $$$$=\underset{\boldsymbol{{r}}=\mathrm{0}} {\overset{\mathrm{7}} {\sum}}\left(−\mathrm{1}\right)^{\boldsymbol{{r}}} \overset{\mathrm{7}} {\boldsymbol{{C}}}_{\boldsymbol{{r}}} \left[\int\boldsymbol{{m}}^{\mathrm{2}\boldsymbol{{r}}+\mathrm{8}} \boldsymbol{{dm}}\right] \\ $$$$=\underset{\boldsymbol{{r}}=\mathrm{0}} {\overset{\mathrm{7}} {\sum}}\left(−\mathrm{1}\right)^{\boldsymbol{{r}}} \overset{\mathrm{7}} {\boldsymbol{{C}}}_{\boldsymbol{{r}}} \frac{\left(\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)\right)^{\mathrm{2}\boldsymbol{{r}}+\mathrm{9}} }{\mathrm{2}\boldsymbol{{r}}+\mathrm{9}}.+\boldsymbol{{k}} \\ $$
