
Question Number 84843 by M±th+et£s last updated on 16/Mar/20
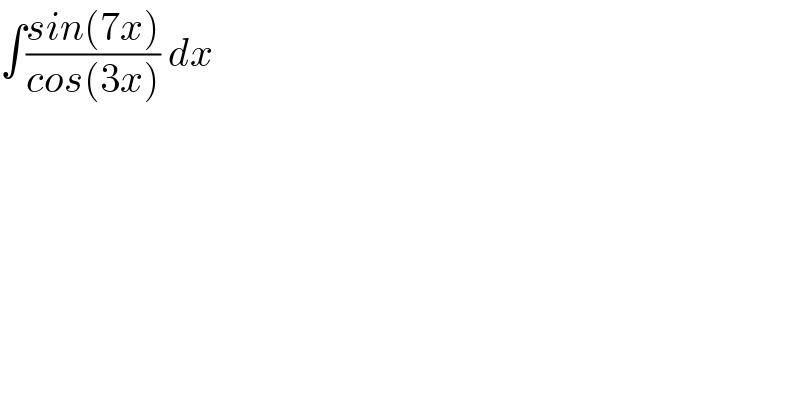
$$\int\frac{{sin}\left(\mathrm{7}{x}\right)}{{cos}\left(\mathrm{3}{x}\right)}\:{dx} \\ $$
Commented by jagoll last updated on 17/Mar/20
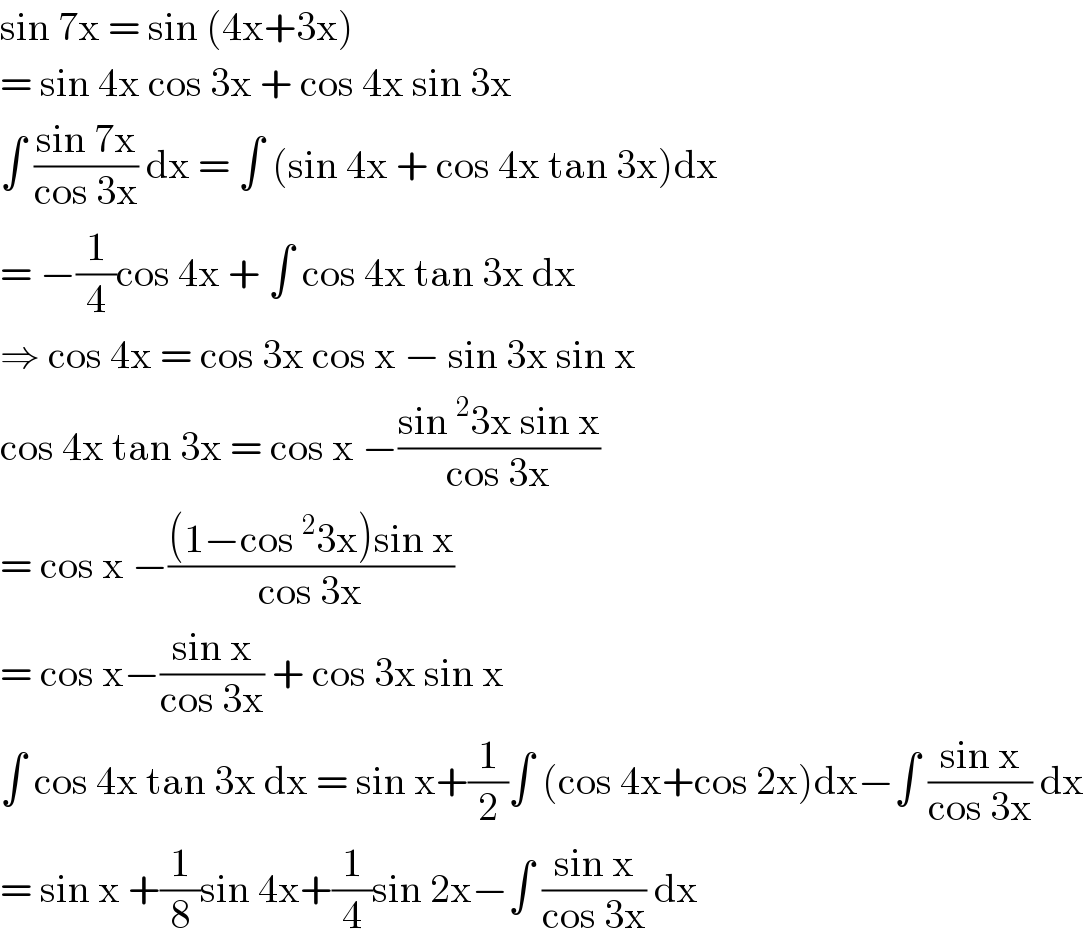
$$\mathrm{sin}\:\mathrm{7x}\:=\:\mathrm{sin}\:\left(\mathrm{4x}+\mathrm{3x}\right)\: \\ $$$$=\:\mathrm{sin}\:\mathrm{4x}\:\mathrm{cos}\:\mathrm{3x}\:+\:\mathrm{cos}\:\mathrm{4x}\:\mathrm{sin}\:\mathrm{3x} \\ $$$$\int\:\frac{\mathrm{sin}\:\mathrm{7x}}{\mathrm{cos}\:\mathrm{3x}}\:\mathrm{dx}\:=\:\int\:\left(\mathrm{sin}\:\mathrm{4x}\:+\:\mathrm{cos}\:\mathrm{4x}\:\mathrm{tan}\:\mathrm{3x}\right)\mathrm{dx} \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:\mathrm{4x}\:+\:\int\:\mathrm{cos}\:\mathrm{4x}\:\mathrm{tan}\:\mathrm{3x}\:\mathrm{dx} \\ $$$$\Rightarrow\:\mathrm{cos}\:\mathrm{4x}\:=\:\mathrm{cos}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{x}\:−\:\mathrm{sin}\:\mathrm{3x}\:\mathrm{sin}\:\mathrm{x} \\ $$$$\mathrm{cos}\:\mathrm{4x}\:\mathrm{tan}\:\mathrm{3x}\:=\:\mathrm{cos}\:\mathrm{x}\:−\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{3x}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{3x}} \\ $$$$=\:\mathrm{cos}\:\mathrm{x}\:−\frac{\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{3x}\right)\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{3x}} \\ $$$$=\:\mathrm{cos}\:\mathrm{x}−\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{3x}}\:+\:\mathrm{cos}\:\mathrm{3x}\:\mathrm{sin}\:\mathrm{x} \\ $$$$\int\:\mathrm{cos}\:\mathrm{4x}\:\mathrm{tan}\:\mathrm{3x}\:\mathrm{dx}\:=\:\mathrm{sin}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\mathrm{cos}\:\mathrm{4x}+\mathrm{cos}\:\mathrm{2x}\right)\mathrm{dx}−\int\:\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{3x}}\:\mathrm{dx} \\ $$$$=\:\mathrm{sin}\:\mathrm{x}\:+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{sin}\:\mathrm{4x}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\mathrm{2x}−\int\:\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{3x}}\:\mathrm{dx} \\ $$
Commented by jagoll last updated on 17/Mar/20
![∫ ((sin x cos x)/(cos 3x cos x)) dx = ∫ ((sin 2x)/(cos 4x+cos 2x)) dx ∫ ((sin 2x)/(2cos^2 2x+cos 2x−1)) dx = −(1/2)∫ (du/(2u^2 +u−1)) [ u = cos 2x ] −(1/2) ∫ (du/((2u−1)(u+1))) so easy to solve](Q84866.png)
$$\int\:\frac{\mathrm{sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{x}}\:\mathrm{dx}\:=\:\int\:\frac{\mathrm{sin}\:\mathrm{2x}}{\mathrm{cos}\:\mathrm{4x}+\mathrm{cos}\:\mathrm{2x}}\:\mathrm{dx} \\ $$$$\int\:\frac{\mathrm{sin}\:\mathrm{2x}}{\mathrm{2cos}\:^{\mathrm{2}} \mathrm{2x}+\mathrm{cos}\:\mathrm{2x}−\mathrm{1}}\:\mathrm{dx}\:= \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{du}}{\mathrm{2u}^{\mathrm{2}} +\mathrm{u}−\mathrm{1}}\:\left[\:\mathrm{u}\:=\:\mathrm{cos}\:\mathrm{2x}\:\right] \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\mathrm{du}}{\left(\mathrm{2u}−\mathrm{1}\right)\left(\mathrm{u}+\mathrm{1}\right)}\: \\ $$$$\mathrm{so}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$
