Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 84163 by john santu last updated on 10/Mar/20

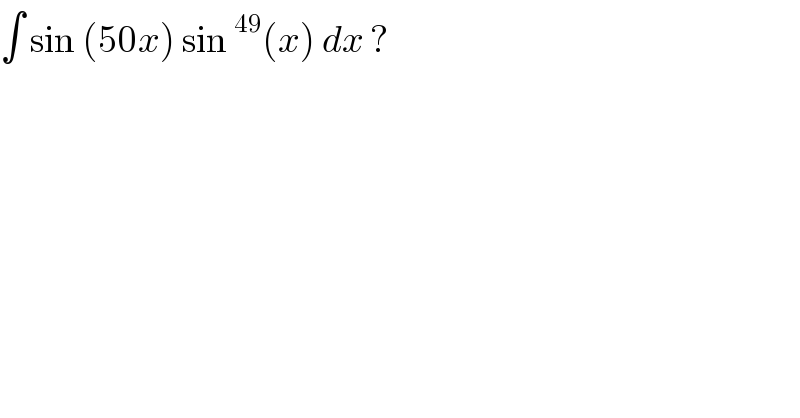
∫ sin (50x) sin^(49) (x) dx ?

$$\int\:\mathrm{sin}\:\left(\mathrm{50}{x}\right)\:\mathrm{sin}\:^{\mathrm{49}} \left({x}\right)\:{dx}\:? \\ $$

Answered by jagoll last updated on 10/Mar/20

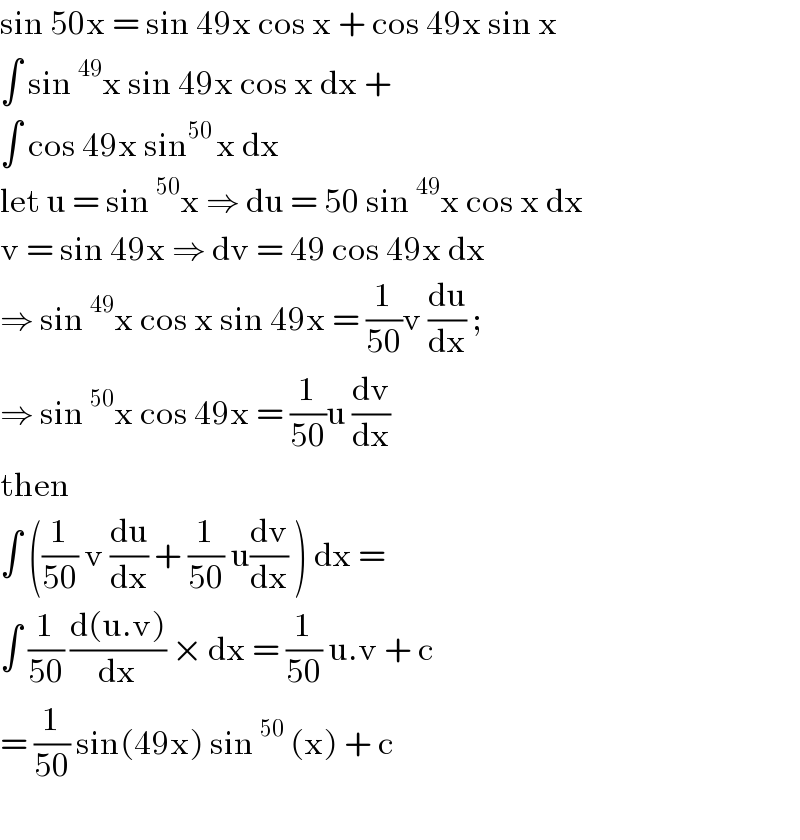
sin 50x = sin 49x cos x + cos 49x sin x ∫ sin^(49) x sin 49x cos x dx + ∫ cos 49x sin^(50 ) x dx let u = sin^(50) x ⇒ du = 50 sin^(49) x cos x dx v = sin 49x ⇒ dv = 49 cos 49x dx ⇒ sin^(49) x cos x sin 49x = (1/(50))v (du/dx) ; ⇒ sin^(50) x cos 49x = (1/(50))u (dv/dx) then ∫ ((1/(50)) v (du/dx) + (1/(50)) u(dv/dx) ) dx = ∫ (1/(50)) ((d(u.v))/dx) × dx = (1/(50)) u.v + c = (1/(50)) sin(49x) sin^(50) (x) + c

$$\mathrm{sin}\:\mathrm{50x}\:=\:\mathrm{sin}\:\mathrm{49x}\:\mathrm{cos}\:\mathrm{x}\:+\:\mathrm{cos}\:\mathrm{49x}\:\mathrm{sin}\:\mathrm{x} \\ $$$$\int\:\mathrm{sin}\:^{\mathrm{49}} \mathrm{x}\:\mathrm{sin}\:\mathrm{49x}\:\mathrm{cos}\:\mathrm{x}\:\mathrm{dx}\:+ \\ $$$$\int\:\mathrm{cos}\:\mathrm{49x}\:\mathrm{sin}^{\mathrm{50}\:} \mathrm{x}\:\mathrm{dx} \\ $$$$\mathrm{let}\:\mathrm{u}\:=\:\mathrm{sin}\:^{\mathrm{50}} \mathrm{x}\:\Rightarrow\:\mathrm{du}\:=\:\mathrm{50}\:\mathrm{sin}\:^{\mathrm{49}} \mathrm{x}\:\mathrm{cos}\:\mathrm{x}\:\mathrm{dx} \\ $$$$\mathrm{v}\:=\:\mathrm{sin}\:\mathrm{49x}\:\Rightarrow\:\mathrm{dv}\:=\:\mathrm{49}\:\mathrm{cos}\:\mathrm{49x}\:\mathrm{dx} \\ $$$$\Rightarrow\:\mathrm{sin}\:^{\mathrm{49}} \mathrm{x}\:\mathrm{cos}\:\mathrm{x}\:\mathrm{sin}\:\mathrm{49x}\:=\:\frac{\mathrm{1}}{\mathrm{50}}\mathrm{v}\:\frac{\mathrm{du}}{\mathrm{dx}}\:;\: \\ $$$$\Rightarrow\:\mathrm{sin}\:^{\mathrm{50}} \mathrm{x}\:\mathrm{cos}\:\mathrm{49x}\:=\:\frac{\mathrm{1}}{\mathrm{50}}\mathrm{u}\:\frac{\mathrm{dv}}{\mathrm{dx}} \\ $$$$\mathrm{then}\: \\ $$$$\int\:\left(\frac{\mathrm{1}}{\mathrm{50}}\:\mathrm{v}\:\frac{\mathrm{du}}{\mathrm{dx}}\:+\:\frac{\mathrm{1}}{\mathrm{50}}\:\mathrm{u}\frac{\mathrm{dv}}{\mathrm{dx}}\:\right)\:\mathrm{dx}\:=\: \\ $$$$\int\:\frac{\mathrm{1}}{\mathrm{50}}\:\frac{\mathrm{d}\left(\mathrm{u}.\mathrm{v}\right)}{\mathrm{dx}}\:×\:\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{50}}\:\mathrm{u}.\mathrm{v}\:+\:\mathrm{c} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{50}}\:\mathrm{sin}\left(\mathrm{49x}\right)\:\mathrm{sin}\:^{\mathrm{50}} \:\left(\mathrm{x}\right)\:+\:\mathrm{c}\: \\ $$$$ \\ $$

Commented by john santu last updated on 10/Mar/20

good sir

$${good}\:{sir} \\ $$

Commented by TANMAY PANACEA last updated on 10/Mar/20

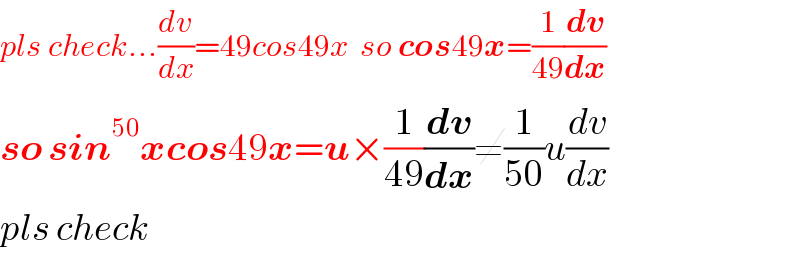
pls check...(dv/dx)=49cos49x so cos49x=(1/(49))(dv/dx) so sin^(50) xcos49x=u×(1/(49))(dv/dx)≠(1/(50))u(dv/dx) pls check

$${pls}\:{check}...\frac{{dv}}{{dx}}=\mathrm{49}{cos}\mathrm{49}{x}\:\:{so}\:\boldsymbol{{cos}}\mathrm{49}\boldsymbol{{x}}=\frac{\mathrm{1}}{\mathrm{49}}\frac{\boldsymbol{{dv}}}{\boldsymbol{{dx}}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{sin}}^{\mathrm{50}} \boldsymbol{{xcos}}\mathrm{49}\boldsymbol{{x}}=\boldsymbol{{u}}×\frac{\mathrm{1}}{\mathrm{49}}\frac{\boldsymbol{{dv}}}{\boldsymbol{{dx}}}\neq\frac{\mathrm{1}}{\mathrm{50}}{u}\frac{{dv}}{{dx}} \\ $$$${pls}\:{check} \\ $$

Answered by TANMAY PANACEA last updated on 10/Mar/20

∫(sin49x.cosx.sin^(49) x+co49xsin^(50) x)dx I_1 =∫sin49x.cosx.sin^(49) xdx I_2 =∫cos49xsin^(50) xdx I=I_1 +I_2 I_1 =sin49x∫sin^(49) xcosxdx−∫[((d sin49x)/dx)∫sin^(49) xcosxdx]dx =sin49x.((sin^(50) x)/(50))−∫49cos49x.((sin^(50) x)/(50))dx =((sin49x.sin^(50) x)/(50))−((49)/(50))I_2 I=I_1 +I_2 =((sin49x.sin^(50) x)/(50))−((49)/(50))I_2 +I_2 I=((sin49x.sin^(50) x)/(50))+(I_2 /(50)) wait pls

$$\int\left({sin}\mathrm{49}{x}.{cosx}.{sin}^{\mathrm{49}} {x}+{co}\mathrm{49}{xsin}^{\mathrm{50}} {x}\right){dx} \\ $$$${I}_{\mathrm{1}} =\int{sin}\mathrm{49}{x}.{cosx}.{sin}^{\mathrm{49}} {xdx} \\ $$$${I}_{\mathrm{2}} =\int{cos}\mathrm{49}{xsin}^{\mathrm{50}} {xdx} \\ $$$${I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} \\ $$$${I}_{\mathrm{1}} ={sin}\mathrm{49}{x}\int{sin}^{\mathrm{49}} {xcosxdx}−\int\left[\frac{{d}\:{sin}\mathrm{49}{x}}{{dx}}\int{sin}^{\mathrm{49}} {xcosxdx}\right]{dx} \\ $$$$={sin}\mathrm{49}{x}.\frac{{sin}^{\mathrm{50}} {x}}{\mathrm{50}}−\int\mathrm{49}{cos}\mathrm{49}{x}.\frac{{sin}^{\mathrm{50}} {x}}{\mathrm{50}}{dx} \\ $$$$=\frac{{sin}\mathrm{49}{x}.{sin}^{\mathrm{50}} {x}}{\mathrm{50}}−\frac{\mathrm{49}}{\mathrm{50}}{I}_{\mathrm{2}} \\ $$$${I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} \\ $$$$\:\:\:=\frac{{sin}\mathrm{49}{x}.{sin}^{\mathrm{50}} {x}}{\mathrm{50}}−\frac{\mathrm{49}}{\mathrm{50}}{I}_{\mathrm{2}} +{I}_{\mathrm{2}} \\ $$$${I}=\frac{{sin}\mathrm{49}{x}.{sin}^{\mathrm{50}} {x}}{\mathrm{50}}+\frac{{I}_{\mathrm{2}} }{\mathrm{50}} \\ $$$${wait}\:{pls} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com