
Question Number 63703 by kaivan.ahmadi last updated on 07/Jul/19
![sin^3 x+cos^3 x=1−(1/2)sin2x :x∈[0,2π]. find x](Q63703.png)
$${sin}^{\mathrm{3}} {x}+{cos}^{\mathrm{3}} {x}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}{x}\:\::{x}\in\left[\mathrm{0},\mathrm{2}\pi\right]. \\ $$$${find}\:\:{x} \\ $$
Commented by Prithwish sen last updated on 08/Jul/19
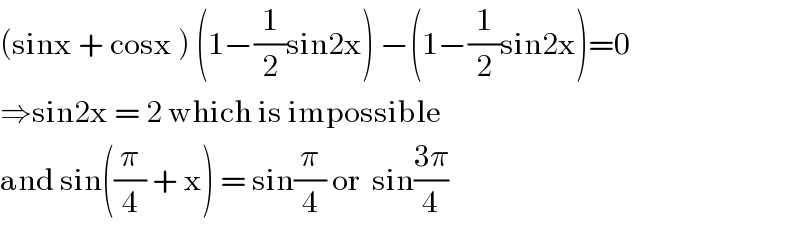
$$\left(\mathrm{sinx}\:+\:\mathrm{cosx}\:\right)\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin2x}\right)\:−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin2x}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin2x}\:=\:\mathrm{2}\:\mathrm{which}\:\mathrm{is}\:\mathrm{impossible} \\ $$$$\mathrm{and}\:\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\:+\:\mathrm{x}\right)\:=\:\mathrm{sin}\frac{\pi}{\mathrm{4}}\:\mathrm{or}\:\:\mathrm{sin}\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$
Commented by kaivan.ahmadi last updated on 08/Jul/19
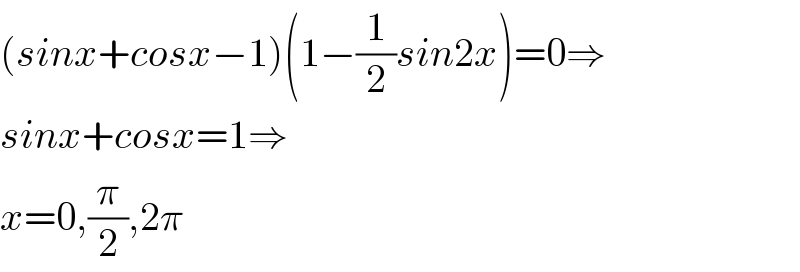
$$\left({sinx}+{cosx}−\mathrm{1}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}{x}\right)=\mathrm{0}\Rightarrow \\ $$$${sinx}+{cosx}=\mathrm{1}\Rightarrow \\ $$$${x}=\mathrm{0},\frac{\pi}{\mathrm{2}},\mathrm{2}\pi \\ $$
Answered by MJS last updated on 07/Jul/19
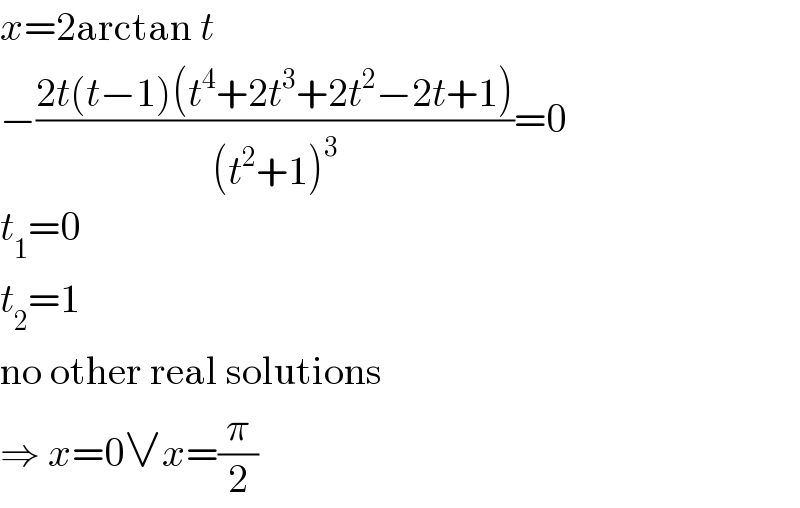
$${x}=\mathrm{2arctan}\:{t} \\ $$$$−\frac{\mathrm{2}{t}\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }=\mathrm{0} \\ $$$${t}_{\mathrm{1}} =\mathrm{0} \\ $$$${t}_{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{no}\:\mathrm{other}\:\mathrm{real}\:\mathrm{solutions} \\ $$$$\Rightarrow\:{x}=\mathrm{0}\vee{x}=\frac{\pi}{\mathrm{2}} \\ $$
Commented by kaivan.ahmadi last updated on 08/Jul/19
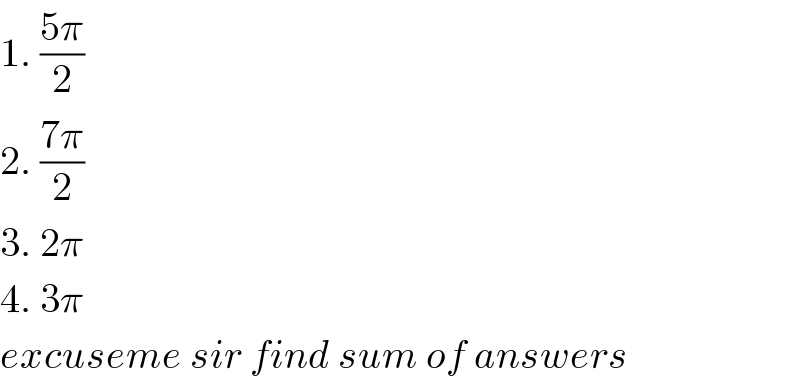
$$\mathrm{1}.\:\frac{\mathrm{5}\pi}{\mathrm{2}} \\ $$$$\mathrm{2}.\:\frac{\mathrm{7}\pi}{\mathrm{2}} \\ $$$$\mathrm{3}.\:\mathrm{2}\pi \\ $$$$\mathrm{4}.\:\mathrm{3}\pi \\ $$$${excuseme}\:{sir}\:{find}\:{sum}\:{of}\:{answers} \\ $$
Commented by kaivan.ahmadi last updated on 08/Jul/19
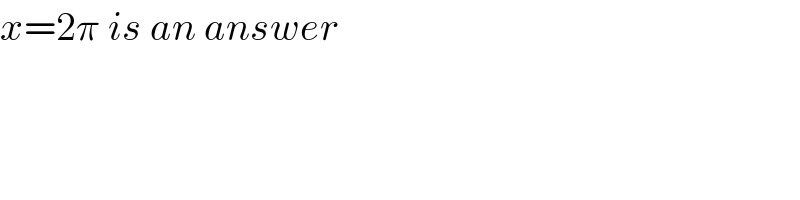
$${x}=\mathrm{2}\pi\:{is}\:{an}\:{answer} \\ $$
Commented by MJS last updated on 08/Jul/19
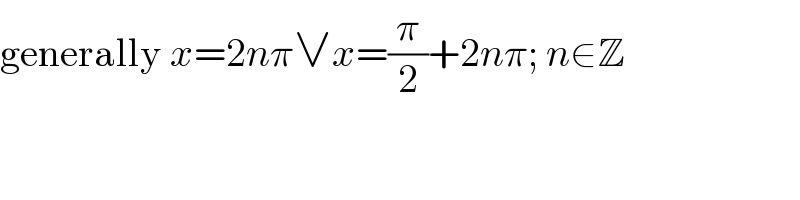
$$\mathrm{generally}\:{x}=\mathrm{2}{n}\pi\vee{x}=\frac{\pi}{\mathrm{2}}+\mathrm{2}{n}\pi;\:{n}\in\mathbb{Z} \\ $$
Commented by MJS last updated on 08/Jul/19
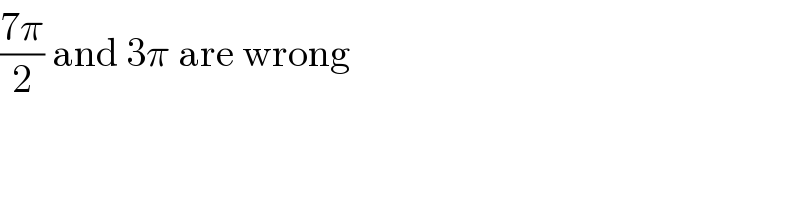
$$\frac{\mathrm{7}\pi}{\mathrm{2}}\:\mathrm{and}\:\mathrm{3}\pi\:\mathrm{are}\:\mathrm{wrong} \\ $$
Commented by kaivan.ahmadi last updated on 08/Jul/19
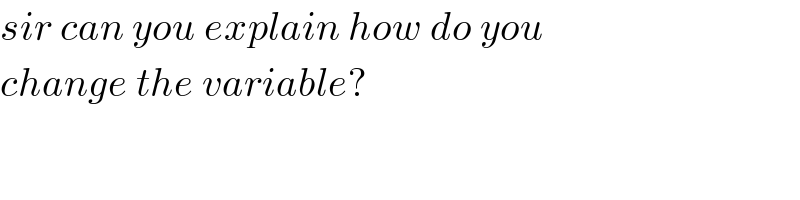
$${sir}\:{can}\:{you}\:{explain}\:{how}\:{do}\:{you} \\ $$$${change}\:{the}\:{variable}? \\ $$
Commented by MJS last updated on 08/Jul/19

$$\mathrm{the}\:\mathrm{substitution}\:{x}=\mathrm{2arctan}\:{t}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\mathrm{sin}\:{x}\:=\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{cos}\:{x}\:=−\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$
Commented by kaivan.ahmadi last updated on 08/Jul/19

$${thanks}\:{sir} \\ $$
