
Question Number 167223 by cortano1 last updated on 10/Mar/22
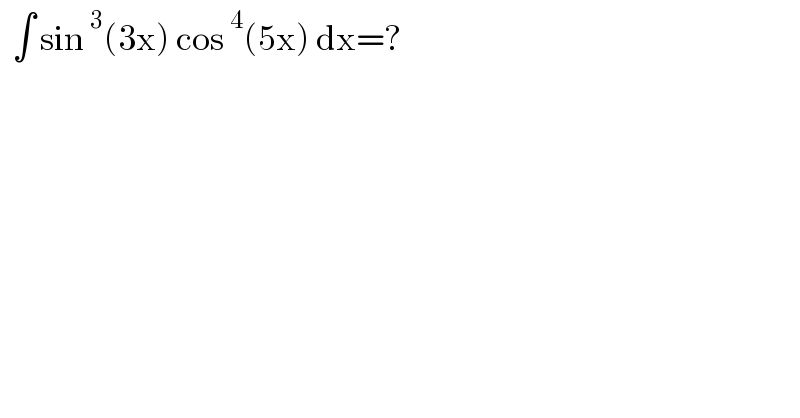
$$\:\:\int\:\mathrm{sin}\:^{\mathrm{3}} \left(\mathrm{3x}\right)\:\mathrm{cos}\:^{\mathrm{4}} \left(\mathrm{5x}\right)\:\mathrm{dx}=? \\ $$
Commented by greogoury55 last updated on 10/Mar/22
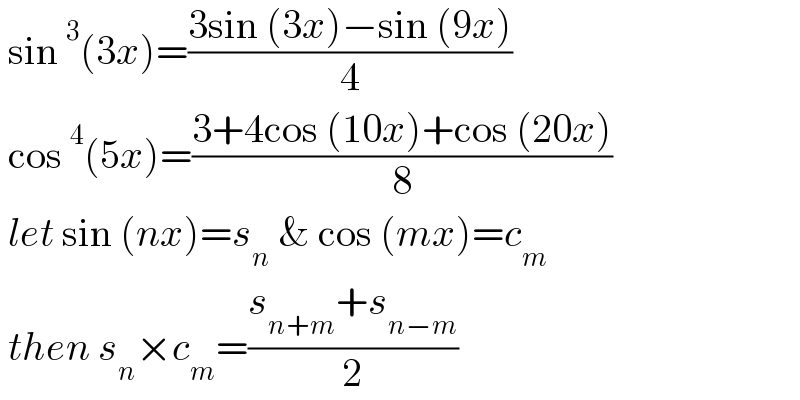
$$\:\mathrm{sin}\:^{\mathrm{3}} \left(\mathrm{3}{x}\right)=\frac{\mathrm{3sin}\:\left(\mathrm{3}{x}\right)−\mathrm{sin}\:\left(\mathrm{9}{x}\right)}{\mathrm{4}} \\ $$$$\:\mathrm{cos}\:^{\mathrm{4}} \left(\mathrm{5}{x}\right)=\frac{\mathrm{3}+\mathrm{4cos}\:\left(\mathrm{10}{x}\right)+\mathrm{cos}\:\left(\mathrm{20}{x}\right)}{\mathrm{8}} \\ $$$$\:{let}\:\mathrm{sin}\:\left({nx}\right)={s}_{{n}} \:\&\:\mathrm{cos}\:\left({mx}\right)={c}_{{m}} \\ $$$$\:{then}\:{s}_{{n}} ×{c}_{{m}} =\frac{{s}_{{n}+{m}} +{s}_{{n}−{m}} }{\mathrm{2}} \\ $$
Commented by MJS_new last updated on 10/Mar/22
![sin^3 3x cos^4 5x = [sin x =s∧cos x =c] =−c^4 (c^2 −1)(4c^2 −1)^3 (16c^4 −20c^2 +5)^4 s we can use t=cos x and get ∫t^4 (t^2 −1)(4t^2 −1)^3 (16t^4 −20t^2 +5)^4 dt which has to be expanded...](Q167228.png)
$$\mathrm{sin}^{\mathrm{3}} \:\mathrm{3}{x}\:\mathrm{cos}^{\mathrm{4}} \:\mathrm{5}{x}\:= \\ $$$$\:\:\:\:\:\left[\mathrm{sin}\:{x}\:={s}\wedge\mathrm{cos}\:{x}\:={c}\right] \\ $$$$=−{c}^{\mathrm{4}} \left({c}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{4}{c}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{16}{c}^{\mathrm{4}} −\mathrm{20}{c}^{\mathrm{2}} +\mathrm{5}\right)^{\mathrm{4}} {s} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{use}\:{t}=\mathrm{cos}\:{x}\:\mathrm{and}\:\mathrm{get} \\ $$$$\int{t}^{\mathrm{4}} \left({t}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{4}{t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{16}{t}^{\mathrm{4}} −\mathrm{20}{t}^{\mathrm{2}} +\mathrm{5}\right)^{\mathrm{4}} {dt} \\ $$$$\mathrm{which}\:\mathrm{has}\:\mathrm{to}\:\mathrm{be}\:\mathrm{expanded}... \\ $$
Commented by cortano1 last updated on 10/Mar/22

