
Question Number 196037 by cortano12 last updated on 16/Aug/23
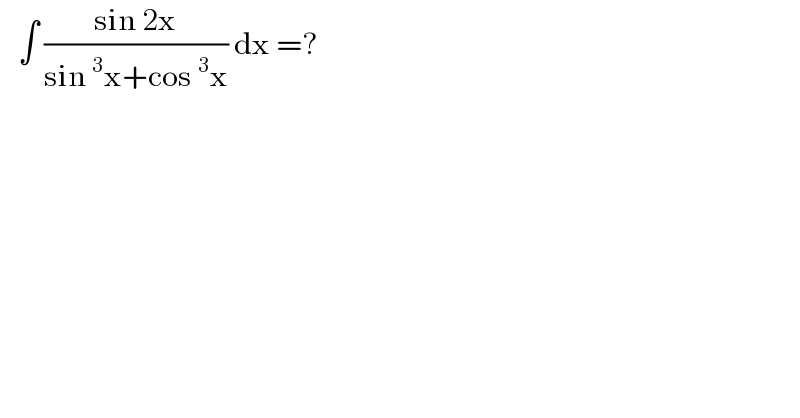
$$\:\:\:\int\:\frac{\mathrm{sin}\:\mathrm{2x}}{\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}}\:\mathrm{dx}\:=? \\ $$
Answered by Frix last updated on 16/Aug/23
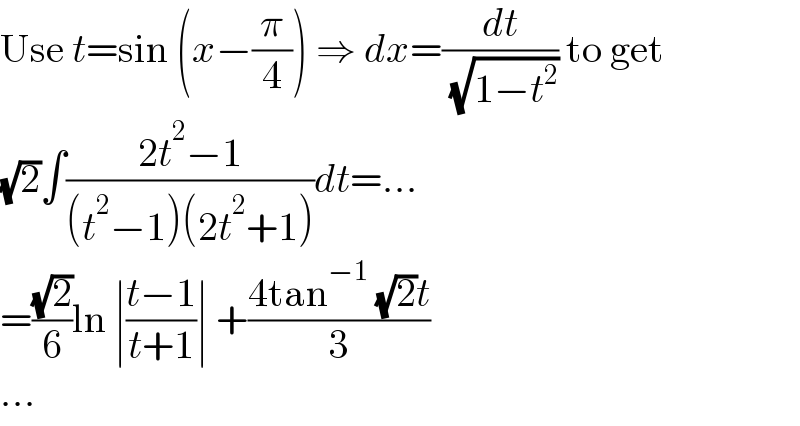
$$\mathrm{Use}\:{t}=\mathrm{sin}\:\left({x}−\frac{\pi}{\mathrm{4}}\right)\:\Rightarrow\:{dx}=\frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:\mathrm{to}\:\mathrm{get} \\ $$$$\sqrt{\mathrm{2}}\int\frac{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}\right)}{dt}=... \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{6}}\mathrm{ln}\:\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid\:+\frac{\mathrm{4tan}^{−\mathrm{1}} \:\sqrt{\mathrm{2}}{t}}{\mathrm{3}} \\ $$$$... \\ $$
Answered by dimentri last updated on 17/Aug/23

