
Question Number 195254 by Spillover last updated on 28/Jul/23

$$\int\frac{\mathrm{sin}\:^{\mathrm{2}} {x}\mathrm{cos}\:^{\mathrm{2}} {x}}{\left(\mathrm{sin}\:^{\mathrm{5}} {x}+\mathrm{cos}\:^{\mathrm{3}} {x}\mathrm{sin}\:^{\mathrm{2}} {x}+\mathrm{sin}\:^{\mathrm{3}} {x}\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{cos}\:^{\mathrm{5}} {x}\right)}{dx} \\ $$
Commented by Frix last updated on 28/Jul/23
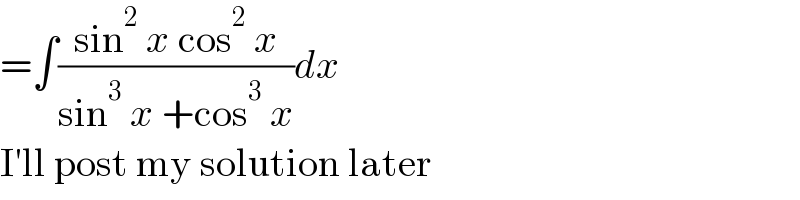
$$=\int\frac{\mathrm{sin}^{\mathrm{2}} \:{x}\:\mathrm{cos}^{\mathrm{2}} \:{x}}{\mathrm{sin}^{\mathrm{3}} \:{x}\:+\mathrm{cos}^{\mathrm{3}} \:{x}}{dx} \\ $$$$\mathrm{I}'\mathrm{ll}\:\mathrm{post}\:\mathrm{my}\:\mathrm{solution}\:\mathrm{later} \\ $$
Answered by Frix last updated on 28/Jul/23
![∫((sin^2 x cos^2 x)/(sin^3 x +cos^3 x))dx =^(t=sin x +cos x) =(1/2)∫(((t^2 −1)^2 )/(t(3−t^2 )(√(2−t^2 ))))dt=_( show this in detail]) ^([sorry no time to) =−(1/2)∫(t/( (√(2−t^2 ))))dt+(1/6)∫(dt/(t(√(2−t^2 ))))−(2/3)∫(t/((t^2 −3)(√(2−t^2 ))))dt= =((√(2−t^2 ))/2)+((√2)/(12))ln ∣(((√(2−t^2 ))−(√2))/t)∣ −(2/3)tan^(−1) (√(2−t^2 )) Now insert t=sin x +cos x =(√2)sin (x+(π/4))](Q195270.png)
$$\int\frac{\mathrm{sin}^{\mathrm{2}} \:{x}\:\mathrm{cos}^{\mathrm{2}} \:{x}}{\mathrm{sin}^{\mathrm{3}} \:{x}\:+\mathrm{cos}^{\mathrm{3}} \:{x}}{dx}\:\overset{{t}=\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}} {=} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{{t}\left(\mathrm{3}−{t}^{\mathrm{2}} \right)\sqrt{\mathrm{2}−{t}^{\mathrm{2}} }}{dt}=_{\left.\:\mathrm{show}\:\mathrm{this}\:\mathrm{in}\:\mathrm{detail}\right]} ^{\left[\mathrm{sorry}\:\mathrm{no}\:\mathrm{time}\:\mathrm{to}\right.} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{t}}{\:\sqrt{\mathrm{2}−{t}^{\mathrm{2}} }}{dt}+\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{dt}}{{t}\sqrt{\mathrm{2}−{t}^{\mathrm{2}} }}−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{t}}{\left({t}^{\mathrm{2}} −\mathrm{3}\right)\sqrt{\mathrm{2}−{t}^{\mathrm{2}} }}{dt}= \\ $$$$=\frac{\sqrt{\mathrm{2}−{t}^{\mathrm{2}} }}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{12}}\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{2}−{t}^{\mathrm{2}} }−\sqrt{\mathrm{2}}}{{t}}\mid\:−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \:\sqrt{\mathrm{2}−{t}^{\mathrm{2}} } \\ $$$$\mathrm{Now}\:\mathrm{insert}\:{t}=\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}\:=\sqrt{\mathrm{2}}\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right) \\ $$
