Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 130423 by john_santu last updated on 25/Jan/21

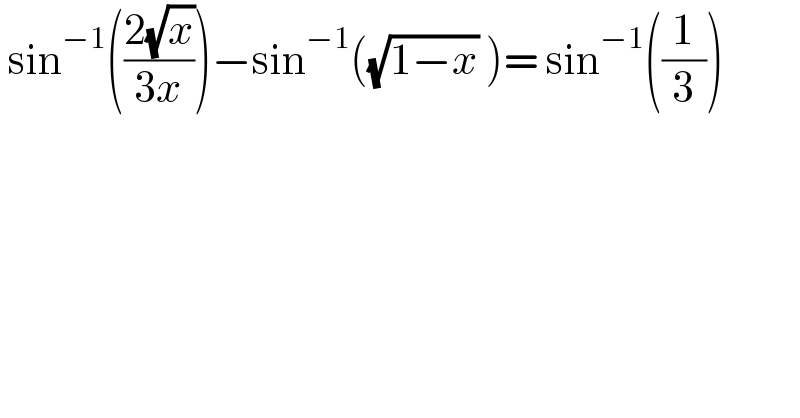
sin^(−1) (((2(√x))/(3x)))−sin^(−1) ((√(1−x)) )= sin^(−1) ((1/3))

$$\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{{x}}}{\mathrm{3}{x}}\right)−\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{1}−{x}}\:\right)=\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$

Answered by liberty last updated on 25/Jan/21

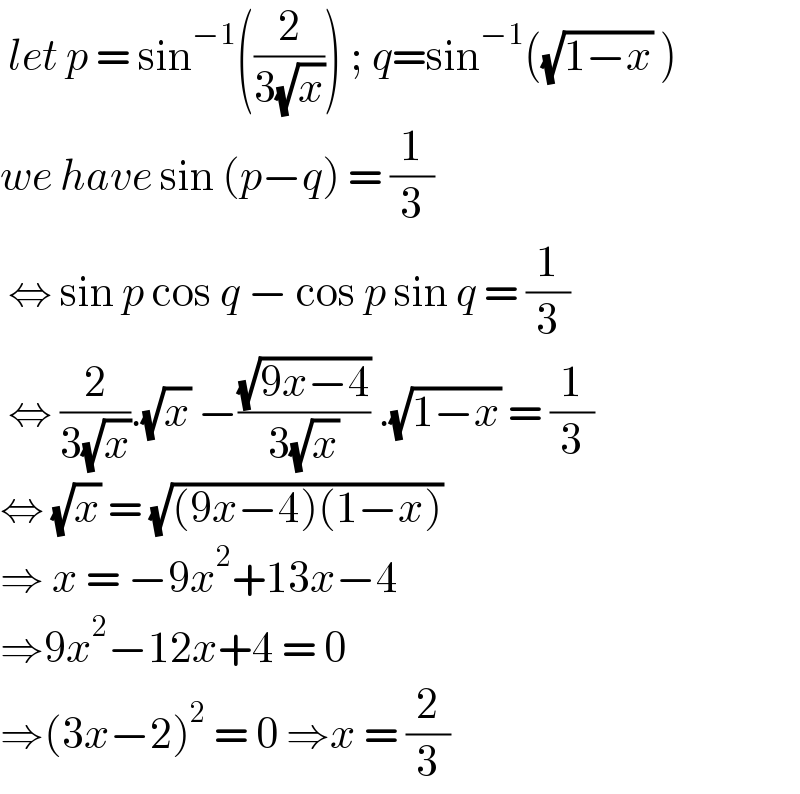
let p = sin^(−1) ((2/(3(√x)))) ; q=sin^(−1) ((√(1−x)) ) we have sin (p−q) = (1/3) ⇔ sin p cos q − cos p sin q = (1/3) ⇔ (2/(3(√x))).(√x) −((√(9x−4))/(3(√x))) .(√(1−x)) = (1/3) ⇔ (√x) = (√((9x−4)(1−x))) ⇒ x = −9x^2 +13x−4 ⇒9x^2 −12x+4 = 0 ⇒(3x−2)^2 = 0 ⇒x = (2/3)

$$\:{let}\:{p}\:=\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{3}\sqrt{{x}}}\right)\:;\:{q}=\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{1}−{x}}\:\right) \\ $$$${we}\:{have}\:\mathrm{sin}\:\left({p}−{q}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\:\Leftrightarrow\:\mathrm{sin}\:{p}\:\mathrm{cos}\:{q}\:−\:\mathrm{cos}\:{p}\:\mathrm{sin}\:{q}\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\:\Leftrightarrow\:\frac{\mathrm{2}}{\mathrm{3}\sqrt{{x}}}.\sqrt{{x}}\:−\frac{\sqrt{\mathrm{9}{x}−\mathrm{4}}}{\mathrm{3}\sqrt{{x}}}\:.\sqrt{\mathrm{1}−{x}}\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Leftrightarrow\:\sqrt{{x}}\:=\:\sqrt{\left(\mathrm{9}{x}−\mathrm{4}\right)\left(\mathrm{1}−{x}\right)} \\ $$$$\Rightarrow\:{x}\:=\:−\mathrm{9}{x}^{\mathrm{2}} +\mathrm{13}{x}−\mathrm{4} \\ $$$$\Rightarrow\mathrm{9}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{4}\:=\:\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{3}{x}−\mathrm{2}\right)^{\mathrm{2}} \:=\:\mathrm{0}\:\Rightarrow{x}\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com