
Question Number 126700 by Eric002 last updated on 23/Dec/20
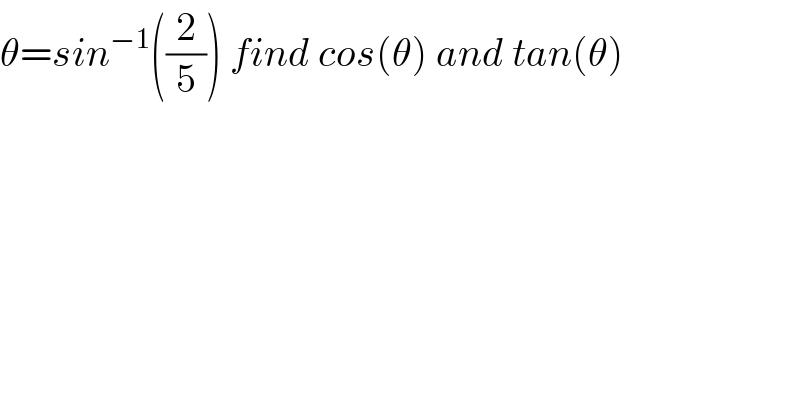
$$\theta={sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{5}}\right)\:{find}\:{cos}\left(\theta\right)\:{and}\:{tan}\left(\theta\right) \\ $$$$ \\ $$
Answered by akornes last updated on 23/Dec/20
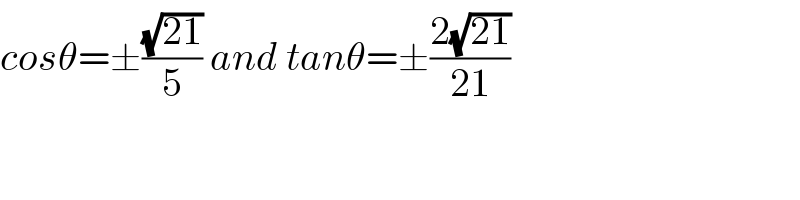
$${cos}\theta=\pm\frac{\sqrt{\mathrm{21}}}{\mathrm{5}}\:{and}\:{tan}\theta=\pm\frac{\mathrm{2}\sqrt{\mathrm{21}}}{\mathrm{21}} \\ $$
Commented by MJS_new last updated on 23/Dec/20
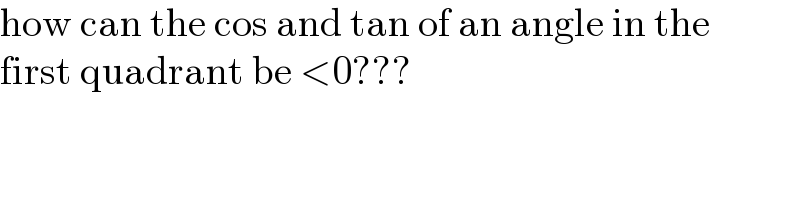
$$\mathrm{how}\:\mathrm{can}\:\mathrm{the}\:\mathrm{cos}\:\mathrm{and}\:\mathrm{tan}\:\mathrm{of}\:\mathrm{an}\:\mathrm{angle}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{first}\:\mathrm{quadrant}\:\mathrm{be}\:<\mathrm{0}??? \\ $$
Answered by MJS_new last updated on 23/Dec/20
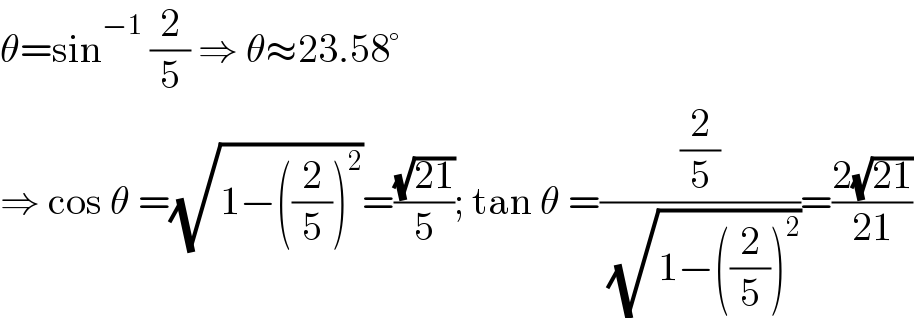
$$\theta=\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{2}}{\mathrm{5}}\:\Rightarrow\:\theta\approx\mathrm{23}.\mathrm{58}° \\ $$$$\Rightarrow\:\mathrm{cos}\:\theta\:=\sqrt{\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{5}}\right)^{\mathrm{2}} }=\frac{\sqrt{\mathrm{21}}}{\mathrm{5}};\:\mathrm{tan}\:\theta\:=\frac{\frac{\mathrm{2}}{\mathrm{5}}}{\:\sqrt{\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{5}}\right)^{\mathrm{2}} }}=\frac{\mathrm{2}\sqrt{\mathrm{21}}}{\mathrm{21}} \\ $$
