
Question Number 14011 by Ruth1 last updated on 26/May/17
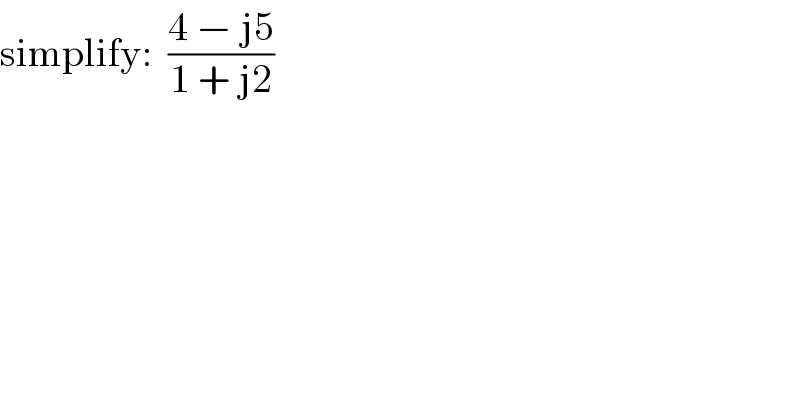
$$\mathrm{simplify}:\:\:\frac{\mathrm{4}\:−\:\mathrm{j5}}{\mathrm{1}\:+\:\mathrm{j2}} \\ $$
Commented by tawa tawa last updated on 26/May/17
![Multiply by the conjugate both numerator and denominator (((4 − j5))/((1 + j2))) × (((1 − j2))/((1 − j2))) = ((4 − j8 − j5 + 10j^2 )/(1^2 − 4j^2 )) = ((4 − j8 − j5 + 10(−1))/(1^2 − 4(−1))) [j^2 = − 1] = ((4 − j8 − j5 − 10)/(1 + 4)) = ((− 6 − j13)/5) = ((−6)/5) − j((13)/5) = − 1.2 − j2.6](Q14013.png)
$$\mathrm{Multiply}\:\mathrm{by}\:\mathrm{the}\:\mathrm{conjugate}\:\mathrm{both}\:\mathrm{numerator}\:\mathrm{and}\:\mathrm{denominator} \\ $$$$\frac{\left(\mathrm{4}\:−\:\mathrm{j5}\right)}{\left(\mathrm{1}\:+\:\mathrm{j2}\right)}\:×\:\frac{\left(\mathrm{1}\:−\:\mathrm{j2}\right)}{\left(\mathrm{1}\:−\:\mathrm{j2}\right)} \\ $$$$=\:\frac{\mathrm{4}\:−\:\mathrm{j8}\:−\:\mathrm{j5}\:+\:\mathrm{10j}^{\mathrm{2}} }{\mathrm{1}^{\mathrm{2}} \:−\:\mathrm{4j}^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{4}\:−\:\mathrm{j8}\:−\:\mathrm{j5}\:+\:\mathrm{10}\left(−\mathrm{1}\right)}{\mathrm{1}^{\mathrm{2}} \:−\:\mathrm{4}\left(−\mathrm{1}\right)}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\mathrm{j}^{\mathrm{2}} \:=\:−\:\mathrm{1}\right] \\ $$$$=\:\frac{\mathrm{4}\:−\:\mathrm{j8}\:−\:\mathrm{j5}\:−\:\mathrm{10}}{\mathrm{1}\:+\:\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\: \\ $$$$=\:\frac{−\:\mathrm{6}\:−\:\mathrm{j13}}{\mathrm{5}}\:\:\:\:\:\:\:\:\:\:\: \\ $$$$=\:\frac{−\mathrm{6}}{\mathrm{5}}\:−\:\mathrm{j}\frac{\mathrm{13}}{\mathrm{5}} \\ $$$$=\:−\:\mathrm{1}.\mathrm{2}\:−\:\mathrm{j2}.\mathrm{6} \\ $$
