
Question Number 152844 by bobhans last updated on 02/Sep/21
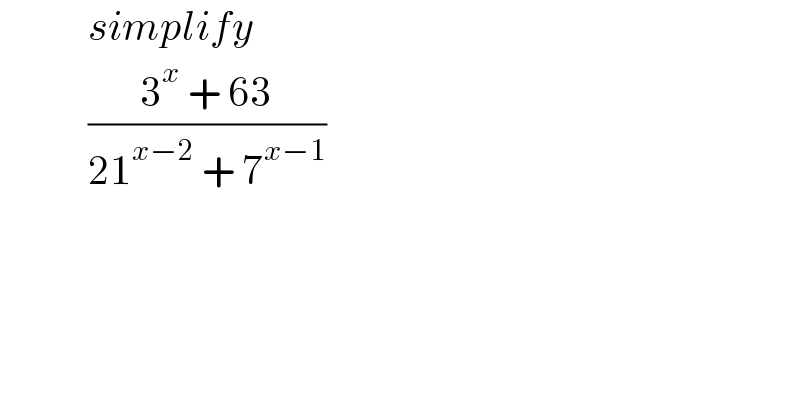
$$\:\:\:\:\:\:\:\:\:\:\:{simplify}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}^{{x}} \:+\:\mathrm{63}}{\mathrm{21}^{{x}−\mathrm{2}} \:+\:\mathrm{7}^{{x}−\mathrm{1}} }\: \\ $$
Answered by Rasheed.Sindhi last updated on 02/Sep/21
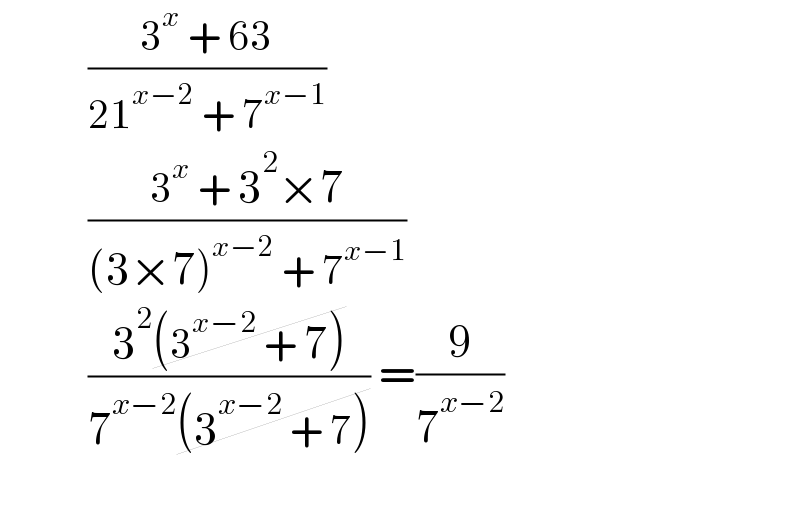
$$\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}^{{x}} \:+\:\mathrm{63}}{\mathrm{21}^{{x}−\mathrm{2}} \:+\:\mathrm{7}^{{x}−\mathrm{1}} }\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}^{{x}} \:+\:\mathrm{3}^{\mathrm{2}} ×\mathrm{7}}{\left(\mathrm{3}×\mathrm{7}\right)^{{x}−\mathrm{2}} \:+\:\mathrm{7}^{{x}−\mathrm{1}} }\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}^{\mathrm{2}} \cancel{\left(\mathrm{3}^{{x}−\mathrm{2}} \:+\:\mathrm{7}\right)}}{\mathrm{7}^{{x}−\mathrm{2}} \cancel{\left(\mathrm{3}^{{x}−\mathrm{2}} \:+\:\mathrm{7}\right)}}\:=\frac{\mathrm{9}}{\mathrm{7}^{{x}−\mathrm{2}} } \\ $$$$ \\ $$
