
Question Number 155265 by SANOGO last updated on 28/Sep/21

$${si}\:{E}\:{est}\:{la}\:{fonction}\:{partie}\:{entiere}\:,{et}\:{n}\:{un}\:{entier}\:{naturel} \\ $$$${alors}\:{I}=\int_{{o}} ^{{n}} {E}\left({x}\right)\:{vaut}? \\ $$
Answered by puissant last updated on 28/Sep/21
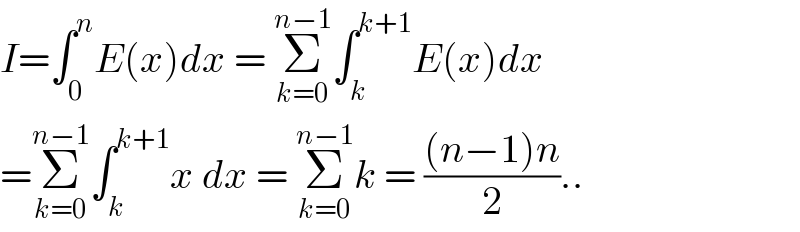
$${I}=\int_{\mathrm{0}} ^{{n}} {E}\left({x}\right){dx}\:=\:\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\int_{{k}} ^{{k}+\mathrm{1}} {E}\left({x}\right){dx} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\int_{{k}} ^{{k}+\mathrm{1}} {x}\:{dx}\:=\:\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{k}\:=\:\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}.. \\ $$
Commented by SANOGO last updated on 28/Sep/21
$${merci}\:{bien}\:{tjrs}\:{le}\:{puissant} \\ $$
