Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 213468 by universe last updated on 06/Nov/24

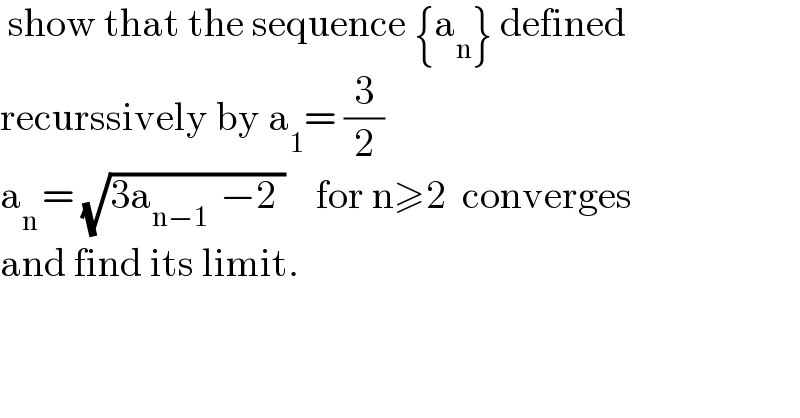
show that the sequence {a_n } defined recurssively by a_1 = (3/2) a_(n ) = (√(3a_(n−1 ) −2 )) for n≥2 converges and find its limit.

$$\:\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{sequence}\:\left\{\mathrm{a}_{\mathrm{n}} \right\}\:\mathrm{defined}\: \\ $$$$\mathrm{recurssively}\:\mathrm{by}\:\mathrm{a}_{\mathrm{1}} =\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{a}_{\mathrm{n}\:} =\:\sqrt{\mathrm{3a}_{\mathrm{n}−\mathrm{1}\:} \:−\mathrm{2}\:}\:\:\:\:\mathrm{for}\:\mathrm{n}\geqslant\mathrm{2}\:\:\mathrm{converges}\: \\ $$$$\mathrm{and}\:\mathrm{find}\:\mathrm{its}\:\mathrm{limit}. \\ $$

Answered by issac last updated on 06/Nov/24

a_2 =(√(3a_1 −2))=(√((9/2)−2))=((√(10))/2) a_1 <a_2 ....true and let′s assume a_(k+1) <a_(k+2) , k∈Z (√(3a_k −2))<(√(3a_(k+1) −2)) ∴a_k <a_(k+1) ....true thus we can conclude that a_(n ) is ′′Monotonic Increase Sequence′′.. and Next we must show that sequence a_(n ) is Bounded or Not step 1. Let′s show that a_n inductively a_n ≤2 a_1 =(3/2)≤2 and if a_n ≤2 → a_(n+1) ≤2 a_(n+1) =(√(3a_n −2))≤2 ∴ a_n ≤2 so Sequence {a_n } is bounded lim_(n→∞) a_n =2 Q.E.D

$${a}_{\mathrm{2}} =\sqrt{\mathrm{3}{a}_{\mathrm{1}} −\mathrm{2}}=\sqrt{\frac{\mathrm{9}}{\mathrm{2}}−\mathrm{2}}=\frac{\sqrt{\mathrm{10}}}{\mathrm{2}} \\ $$$${a}_{\mathrm{1}} <{a}_{\mathrm{2}} \:....\mathrm{true} \\ $$$$\mathrm{and}\:\mathrm{let}'\mathrm{s}\:\mathrm{assume}\:\:{a}_{{k}+\mathrm{1}} <{a}_{{k}+\mathrm{2}} \:,\:{k}\in\mathbb{Z} \\ $$$$\:\sqrt{\mathrm{3}{a}_{{k}} −\mathrm{2}}<\sqrt{\mathrm{3}{a}_{{k}+\mathrm{1}} −\mathrm{2}} \\ $$$$\therefore{a}_{{k}} <{a}_{{k}+\mathrm{1}} \:....\mathrm{true} \\ $$$$\mathrm{thus}\:\mathrm{we}\:\mathrm{can}\:\mathrm{conclude}\:\mathrm{that}\:{a}_{{n}\:} \mathrm{is} \\ $$$$\:''\mathrm{Monotonic}\:\mathrm{Increase}\:\mathrm{Sequence}''.. \\ $$$$\mathrm{and}\:\mathrm{Next}\:\mathrm{we}\:\mathrm{must}\:\mathrm{show}\:\mathrm{that}\:\mathrm{sequence} \\ $$$${a}_{{n}\:} \mathrm{is}\:\boldsymbol{\mathrm{Bounded}}\:\boldsymbol{\mathrm{or}}\:\boldsymbol{\mathrm{Not}} \\ $$$$\boldsymbol{\mathrm{step}}\:\mathrm{1}. \\ $$$$\mathrm{Let}'\mathrm{s}\:\mathrm{show}\:\mathrm{that}\:{a}_{{n}} \:\mathrm{inductively}\:\:{a}_{{n}} \leq\mathrm{2} \\ $$$${a}_{\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{2}}\leq\mathrm{2}\:\:\mathrm{and}\:\mathrm{if}\:\:{a}_{{n}} \leq\mathrm{2}\:\:\rightarrow\:{a}_{{n}+\mathrm{1}} \leq\mathrm{2} \\ $$$${a}_{{n}+\mathrm{1}} =\sqrt{\mathrm{3}{a}_{{n}} −\mathrm{2}}\leq\mathrm{2} \\ $$$$\therefore\:{a}_{{n}} \leq\mathrm{2}\:\:\mathrm{so}\:\:\mathrm{Sequence}\:\left\{{a}_{{n}} \right\}\:\mathrm{is}\:\mathrm{bounded} \\ $$$$\:\: \\ $$$$\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{a}_{{n}} =\mathrm{2}\:\:\mathbb{Q}.\mathbb{E}.\mathbb{D} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com