
Question Number 217088 by alcohol last updated on 28/Feb/25
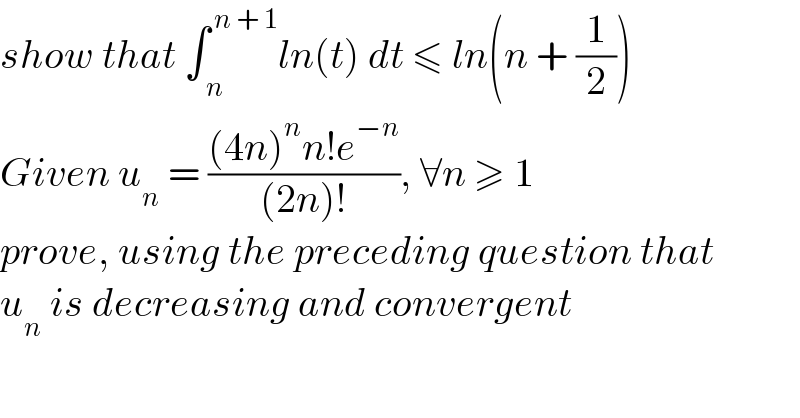
$${show}\:{that}\:\int_{\:{n}} ^{\:{n}\:+\:\mathrm{1}} {ln}\left({t}\right)\:{dt}\:\leqslant\:{ln}\left({n}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${Given}\:{u}_{{n}} \:=\:\frac{\left(\mathrm{4}{n}\right)^{{n}} {n}!{e}^{−{n}} }{\left(\mathrm{2}{n}\right)!},\:\forall{n}\:\geqslant\:\mathrm{1} \\ $$$${prove},\:{using}\:{the}\:{preceding}\:{question}\:{that} \\ $$$${u}_{{n}} \:{is}\:{decreasing}\:{and}\:{convergent} \\ $$
Answered by MrGaster last updated on 01/Mar/25
![Prove:∫_n ^(n+1) ln(t)dt≤ln(n+(1/2)) ∫_n ^(n+1) ln(t)dt=[t ln(t)−t]_n ^(n+1) =((n+1)+ln(n+1)−(n+1)−(n ln(n)−n) =(n+1)ln(n+1)−n ln(n)−1 ln(n+1)≤ln(n)+(1/n) ⊢(n+1)ln(n+1)≤(n+1)(ln(n)+(1/n)) =(n+1)ln(n)+(n+1)(1/n) =(n+1)ln(n)+1(1/n) ∴(n+1)ln(n+1)−n ln(n)−1≤((n+1)ln(n)+1+(1/n))−n ln(n)−1 =ln(n)+(1/n) ∵(1/n)≤ln(1+(1/(2n)))⇒ln(n)+(1/n)≤ln(n)+ln(1+(1/(2n))) =ln(n(1+(1/(2n)))) =ln(n+(1/2)) so, determinant (((∫_n ^(n+1) ln(t)dt≤ln(n+(1/2))))) Give u_n =(((4n)^n n!e^(−n) )/((2n)!)),∀n≥1,Prove that u_n is decreasing and converhgent. Part 1:Prove u_n is decreasing. Consider the ratio: (u_(n+1) /u_n )=((((4(n+1)^(n+1) (n+1)!e^(−(n+1)) )/((2(n+1)!))/(((4n)^n e^(−n) )/((2n)!))) =(((4(n+1))^(n+1) (n+1)e^(−1) )/((4n)^n (2n+2)(2n+1))) =((4^(n+1) (n+1)^(n+1) (n+1)e^(−1) )/(4^n n^n (2n+2)(2n+1))) =((4(n+1)^(n+2) e^(−1) )/(n^n 2(n+1)(2n+1))) =((2(n+1)^(n+1) e^(−1) )/(n^n (2n+1))) ∵(n+1)^(n+1) >n^(n+1) ⇒(((n+1)^(n−1) )/n^n )>1 ∴(u_(n+1) /u_n )<1 for large n,implying u_n is decreasing. Step 2:Prove u_n is convergent.Using stirling′s approximation n!≈(√(2πn))((n/e))^n ⇒u_n =(((4n)^n n!e^(−n) )/((2n)!))≈(((4n)^n (√(2πn))((n/e))^n e^(−n) )/( (√(4πn))(((2n)/e))^(2n) )) =(((4n)^n (√(2πn))n^n e^(−2n) )/( (√(4πn))2^(2n) n^(2n) )) =(((√(2πn))4^n n^n e^(−2n) )/( (√(4πn))2^n n^(2n) )) =(((√(2π))4^n e^(−2n) )/( (√(4π))2^(2n) n^n )) =(((√2)2^(2n) e^(−2n) )/( (√2)2^(2n) n^n )) =(e^(2n) /n^n ) As n→∞,e^(−2n) →0 and n^n →∞,so u_n →0.Thus,u_n is convergent. determinant (((u_n is decreasing and convergent)))](Q217090.png)
$$\mathrm{Prove}:\int_{{n}} ^{{n}+\mathrm{1}} \mathrm{ln}\left({t}\right){dt}\leq\mathrm{ln}\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\int_{{n}} ^{{n}+\mathrm{1}} \mathrm{ln}\left({t}\right){dt}=\left[{t}\:\mathrm{ln}\left({t}\right)−{t}\right]_{{n}} ^{{n}+\mathrm{1}} \\ $$$$=\left(\left({n}+\mathrm{1}\right)+\mathrm{ln}\left({n}+\mathrm{1}\right)−\left({n}+\mathrm{1}\right)−\left({n}\:\mathrm{ln}\left({n}\right)−{n}\right)\right. \\ $$$$=\left({n}+\mathrm{1}\right)\mathrm{ln}\left({n}+\mathrm{1}\right)−{n}\:\mathrm{ln}\left({n}\right)−\mathrm{1} \\ $$$$\mathrm{ln}\left({n}+\mathrm{1}\right)\leq\mathrm{ln}\left({n}\right)+\frac{\mathrm{1}}{{n}}\:\vdash\left({n}+\mathrm{1}\right)\mathrm{ln}\left({n}+\mathrm{1}\right)\leq\left({n}+\mathrm{1}\right)\left(\mathrm{ln}\left({n}\right)+\frac{\mathrm{1}}{{n}}\right) \\ $$$$=\left({n}+\mathrm{1}\right)\mathrm{ln}\left({n}\right)+\left({n}+\mathrm{1}\right)\frac{\mathrm{1}}{{n}} \\ $$$$=\left({n}+\mathrm{1}\right)\mathrm{ln}\left({n}\right)+\mathrm{1}\frac{\mathrm{1}}{{n}} \\ $$$$\therefore\left({n}+\mathrm{1}\right)\mathrm{ln}\left({n}+\mathrm{1}\right)−{n}\:\mathrm{ln}\left({n}\right)−\mathrm{1}\leq\left(\left({n}+\mathrm{1}\right)\mathrm{ln}\left({n}\right)+\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)−{n}\:\mathrm{ln}\left({n}\right)−\mathrm{1} \\ $$$$=\mathrm{ln}\left({n}\right)+\frac{\mathrm{1}}{{n}} \\ $$$$\because\frac{\mathrm{1}}{{n}}\leq\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right)\Rightarrow\mathrm{ln}\left({n}\right)+\frac{\mathrm{1}}{{n}}\leq\mathrm{ln}\left({n}\right)+\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right) \\ $$$$=\mathrm{ln}\left({n}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right)\right) \\ $$$$=\mathrm{ln}\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\mathrm{so},\begin{array}{|c|}{\int_{{n}} ^{{n}+\mathrm{1}} \mathrm{ln}\left({t}\right){dt}\leq\mathrm{ln}\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\\\hline\end{array} \\ $$$$\mathrm{Give}\:{u}_{{n}} =\frac{\left(\mathrm{4}{n}\right)^{{n}} {n}!{e}^{−{n}} }{\left(\mathrm{2}{n}\right)!},\forall{n}\geq\mathrm{1},\mathrm{Prove}\:\mathrm{that}\:{u}_{{n}} \mathrm{is}\:\mathrm{decreasing}\:\mathrm{and}\:\mathrm{converhgent}. \\ $$$$\mathrm{Part}\:\mathrm{1}:\mathrm{Prove}\:{u}_{{n}} \mathrm{is}\:\mathrm{decreasing}. \\ $$$$\mathrm{Consider}\:\mathrm{the}\:\mathrm{ratio}: \\ $$$$\frac{{u}_{{n}+\mathrm{1}} }{{u}_{{n}} }=\frac{\frac{\left(\mathrm{4}\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} \left({n}+\mathrm{1}\right)!{e}^{−\left({n}+\mathrm{1}\right)} \right.}{\left(\mathrm{2}\left({n}+\mathrm{1}\right)!\right.}}{\frac{\left(\mathrm{4}{n}\right)^{{n}} {e}^{−{n}} }{\left(\mathrm{2}{n}\right)!}} \\ $$$$=\frac{\left(\mathrm{4}\left({n}+\mathrm{1}\right)\right)^{{n}+\mathrm{1}} \left({n}+\mathrm{1}\right){e}^{−\mathrm{1}} }{\left(\mathrm{4}{n}\right)^{{n}} \left(\mathrm{2}{n}+\mathrm{2}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{4}^{{n}+\mathrm{1}} \left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} \left({n}+\mathrm{1}\right){e}^{−\mathrm{1}} }{\mathrm{4}^{{n}} {n}^{{n}} \left(\mathrm{2}{n}+\mathrm{2}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{4}\left({n}+\mathrm{1}\right)^{{n}+\mathrm{2}} {e}^{−\mathrm{1}} }{{n}^{{n}} \mathrm{2}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{2}\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} {e}^{−\mathrm{1}} }{{n}^{{n}} \left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$\because\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} >{n}^{{n}+\mathrm{1}} \Rightarrow\frac{\left({n}+\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{{n}} }>\mathrm{1} \\ $$$$\therefore\frac{{u}_{{n}+\mathrm{1}} }{{u}_{{n}} }<\mathrm{1}\:\mathrm{for}\:\mathrm{large}\:{n},\mathrm{implying}\:{u}_{{n}} \mathrm{is}\:\mathrm{decreasing}. \\ $$$$\mathrm{Step}\:\mathrm{2}:\mathrm{Prove}\:{u}_{{n}} \mathrm{is}\:\mathrm{convergent}.\mathrm{Using}\:\mathrm{stirling}'\mathrm{s}\:\mathrm{approximation}\:{n}!\approx\sqrt{\mathrm{2}\pi{n}}\left(\frac{{n}}{{e}}\right)^{{n}} \Rightarrow{u}_{{n}} =\frac{\left(\mathrm{4}{n}\right)^{{n}} {n}!{e}^{−{n}} }{\left(\mathrm{2}{n}\right)!}\approx\frac{\left(\mathrm{4}{n}\right)^{{n}} \sqrt{\mathrm{2}\pi{n}}\left(\frac{{n}}{{e}}\right)^{{n}} {e}^{−{n}} }{\:\sqrt{\mathrm{4}\pi{n}}\left(\frac{\mathrm{2}{n}}{{e}}\right)^{\mathrm{2}{n}} } \\ $$$$=\frac{\left(\mathrm{4}{n}\right)^{{n}} \sqrt{\mathrm{2}\pi{n}}{n}^{{n}} {e}^{−\mathrm{2}{n}} }{\:\sqrt{\mathrm{4}\pi{n}}\mathrm{2}^{\mathrm{2}{n}} {n}^{\mathrm{2}{n}} } \\ $$$$=\frac{\sqrt{\mathrm{2}\pi{n}}\mathrm{4}^{{n}} {n}^{{n}} {e}^{−\mathrm{2}{n}} }{\:\sqrt{\mathrm{4}\pi{n}}\mathrm{2}^{{n}} {n}^{\mathrm{2}{n}} } \\ $$$$=\frac{\sqrt{\mathrm{2}\pi}\mathrm{4}^{{n}} {e}^{−\mathrm{2}{n}} }{\:\sqrt{\mathrm{4}\pi}\mathrm{2}^{\mathrm{2}{n}} {n}^{{n}} } \\ $$$$=\frac{\sqrt{\mathrm{2}}\mathrm{2}^{\mathrm{2}{n}} {e}^{−\mathrm{2}{n}} }{\:\sqrt{\mathrm{2}}\mathrm{2}^{\mathrm{2}{n}} {n}^{{n}} } \\ $$$$=\frac{{e}^{\mathrm{2}{n}} }{{n}^{{n}} } \\ $$$$\mathrm{As}\:{n}\rightarrow\infty,{e}^{−\mathrm{2}{n}} \rightarrow\mathrm{0}\:\mathrm{and}\:{n}^{{n}} \rightarrow\infty,\mathrm{so}\:{u}_{{n}} \rightarrow\mathrm{0}.\mathrm{Thus},{u}_{{n}} \mathrm{is}\:\mathrm{convergent}. \\ $$$$\begin{array}{|c|}{{u}_{{n}} \mathrm{is}\:\mathrm{decreasing}\:\mathrm{and}\:\mathrm{convergent}}\\\hline\end{array} \\ $$
