
Question Number 17779 by Mr easymsn last updated on 10/Jul/17
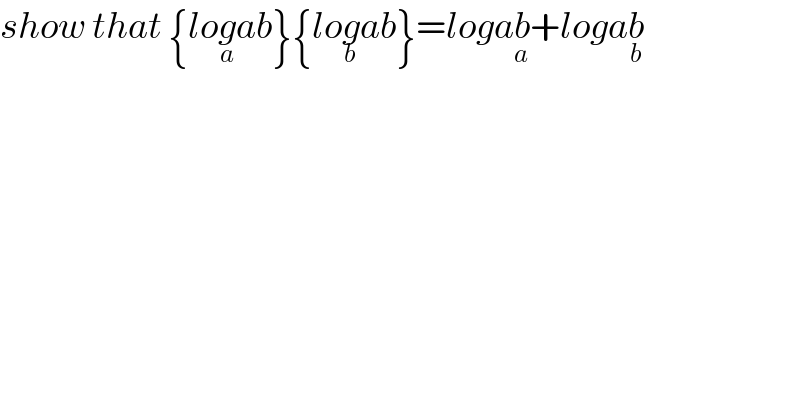
$${show}\:{that}\:\left\{{lo}\underset{{a}} {{g}ab}\right\}\left\{{lo}\underset{{b}} {{g}ab}\right\}={loga}\underset{{a}} {{b}}+{loga}\underset{{b}} {{b}} \\ $$
Answered by Tinkutara last updated on 11/Jul/17
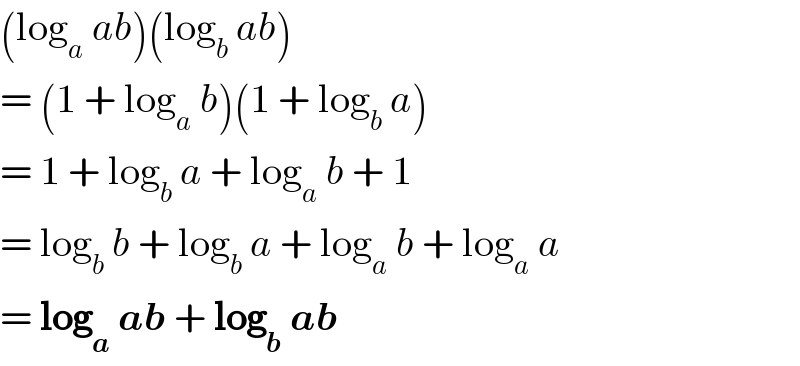
$$\left(\mathrm{log}_{{a}} \:{ab}\right)\left(\mathrm{log}_{{b}} \:{ab}\right) \\ $$$$=\:\left(\mathrm{1}\:+\:\mathrm{log}_{{a}} \:{b}\right)\left(\mathrm{1}\:+\:\mathrm{log}_{{b}} \:{a}\right) \\ $$$$=\:\mathrm{1}\:+\:\mathrm{log}_{{b}} \:{a}\:+\:\mathrm{log}_{{a}} \:{b}\:+\:\mathrm{1} \\ $$$$=\:\mathrm{log}_{{b}} \:{b}\:+\:\mathrm{log}_{{b}} \:{a}\:+\:\mathrm{log}_{{a}} \:{b}\:+\:\mathrm{log}_{{a}} \:{a} \\ $$$$=\:\boldsymbol{\mathrm{log}}_{\boldsymbol{{a}}} \:\boldsymbol{{ab}}\:+\:\boldsymbol{\mathrm{log}}_{\boldsymbol{{b}}} \:\boldsymbol{{ab}} \\ $$
