Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 195364 by Rodier97 last updated on 01/Aug/23

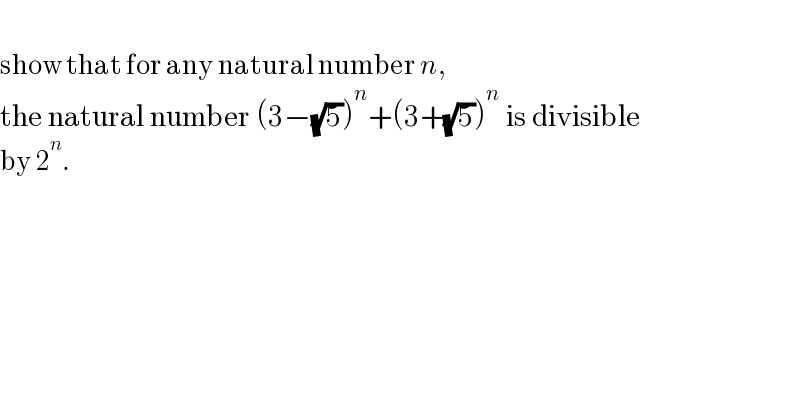
show that for any natural number n, the natural number (3−(√5))^n +(3+(√5))^n is divisible by 2^n .

$$ \\ $$$$\mathrm{show}\:\mathrm{that}\:\mathrm{for}\:\mathrm{any}\:\mathrm{natural}\:\mathrm{number}\:{n},\: \\ $$$$\mathrm{the}\:\mathrm{natural}\:\mathrm{number}\:\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)^{{n}} +\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)^{{n}} \:\mathrm{is}\:\mathrm{divisible} \\ $$$$\mathrm{by}\:\mathrm{2}^{{n}} . \\ $$

Answered by Frix last updated on 31/Jul/23

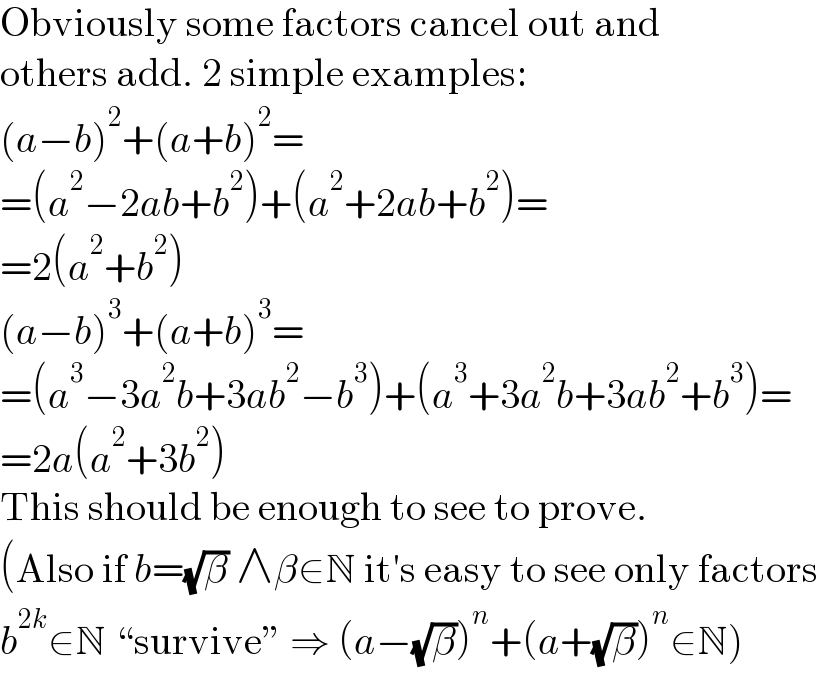
Obviously some factors cancel out and others add. 2 simple examples: (a−b)^2 +(a+b)^2 = =(a^2 −2ab+b^2 )+(a^2 +2ab+b^2 )= =2(a^2 +b^2 ) (a−b)^3 +(a+b)^3 = =(a^3 −3a^2 b+3ab^2 −b^3 )+(a^3 +3a^2 b+3ab^2 +b^3 )= =2a(a^2 +3b^2 ) This should be enough to see to prove. (Also if b=(√β) ∧β∈N it′s easy to see only factors b^(2k) ∈N “survive” ⇒ (a−(√β))^n +(a+(√β))^n ∈N)

$$\mathrm{Obviously}\:\mathrm{some}\:\mathrm{factors}\:\mathrm{cancel}\:\mathrm{out}\:\mathrm{and} \\ $$$$\mathrm{others}\:\mathrm{add}.\:\mathrm{2}\:\mathrm{simple}\:\mathrm{examples}: \\ $$$$\left({a}−{b}\right)^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} = \\ $$$$=\left({a}^{\mathrm{2}} −\mathrm{2}{ab}+{b}^{\mathrm{2}} \right)+\left({a}^{\mathrm{2}} +\mathrm{2}{ab}+{b}^{\mathrm{2}} \right)= \\ $$$$=\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$$$\left({a}−{b}\right)^{\mathrm{3}} +\left({a}+{b}\right)^{\mathrm{3}} = \\ $$$$=\left({a}^{\mathrm{3}} −\mathrm{3}{a}^{\mathrm{2}} {b}+\mathrm{3}{ab}^{\mathrm{2}} −{b}^{\mathrm{3}} \right)+\left({a}^{\mathrm{3}} +\mathrm{3}{a}^{\mathrm{2}} {b}+\mathrm{3}{ab}^{\mathrm{2}} +{b}^{\mathrm{3}} \right)= \\ $$$$=\mathrm{2}{a}\left({a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} \right) \\ $$$$\mathrm{This}\:\mathrm{should}\:\mathrm{be}\:\mathrm{enough}\:\mathrm{to}\:\mathrm{see}\:\mathrm{to}\:\mathrm{prove}. \\ $$$$\left(\mathrm{Also}\:\mathrm{if}\:{b}=\sqrt{\beta}\:\wedge\beta\in\mathbb{N}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{only}\:\mathrm{factors}\right. \\ $$$$\left.{b}^{\mathrm{2}{k}} \in\mathbb{N}\:``\mathrm{survive}''\:\Rightarrow\:\left({a}−\sqrt{\beta}\right)^{{n}} +\left({a}+\sqrt{\beta}\right)^{{n}} \in\mathbb{N}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com