
Question Number 163153 by MathsFan last updated on 04/Jan/22
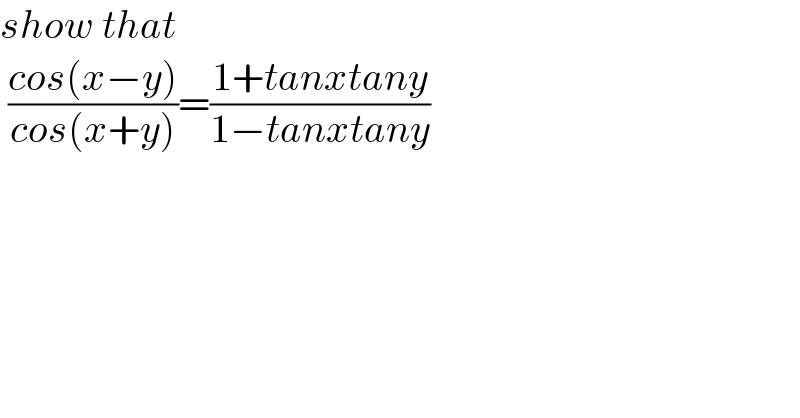
$${show}\:{that} \\ $$$$\:\frac{{cos}\left({x}−{y}\right)}{{cos}\left({x}+{y}\right)}=\frac{\mathrm{1}+{tanxtany}}{\mathrm{1}−{tanxtany}} \\ $$
Answered by cortano1 last updated on 04/Jan/22
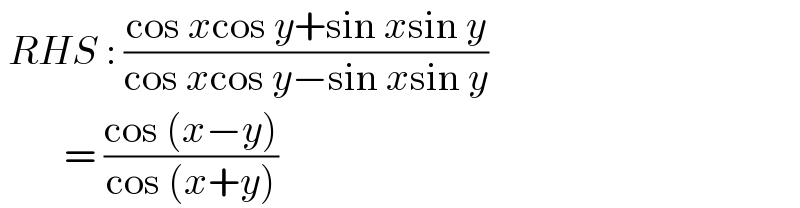
$$\:{RHS}\::\:\frac{\mathrm{cos}\:{x}\mathrm{cos}\:{y}+\mathrm{sin}\:{x}\mathrm{sin}\:{y}}{\mathrm{cos}\:{x}\mathrm{cos}\:{y}−\mathrm{sin}\:{x}\mathrm{sin}\:{y}}\: \\ $$$$\:\:\:\:\:\:\:\:=\:\frac{\mathrm{cos}\:\left({x}−{y}\right)}{\mathrm{cos}\:\left({x}+{y}\right)} \\ $$
Answered by Rasheed.Sindhi last updated on 04/Jan/22

$$\:\frac{{cos}\left({x}−{y}\right)}{{cos}\left({x}+{y}\right)}=\frac{\mathrm{1}+{tanxtany}}{\mathrm{1}−{tanxtany}} \\ $$$$\mathrm{LHS}:\:\frac{{cos}\left({x}−{y}\right)}{{cos}\left({x}+{y}\right)} \\ $$$$=\frac{{cosxcosy}+{sinxsiny}}{{cosxcosy}+{sinxsiny}} \\ $$$$=\frac{\frac{{cosxcosy}+{sinxsiny}}{{cosxcosy}}}{\frac{{cosxcosy}−{sinxsiny}}{{cosxcosy}}} \\ $$$$=\frac{\mathrm{1}+\frac{{sinxsiny}}{{cosxcosy}}}{\mathrm{1}−\frac{{sinxsiny}}{{cosxcosy}}}=\frac{\mathrm{1}+\frac{{sinx}}{{cosx}}\centerdot\frac{{siny}}{{cosy}}}{\mathrm{1}−\frac{{sinx}}{{cosx}}\centerdot\frac{{siny}}{{cosy}}} \\ $$$$=\frac{\mathrm{1}+{tanxtany}}{\mathrm{1}−{tanxtany}}=\mathrm{RHS} \\ $$
Commented by MathsFan last updated on 04/Jan/22

$${merci} \\ $$
