Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 126720 by mathocean1 last updated on 23/Dec/20

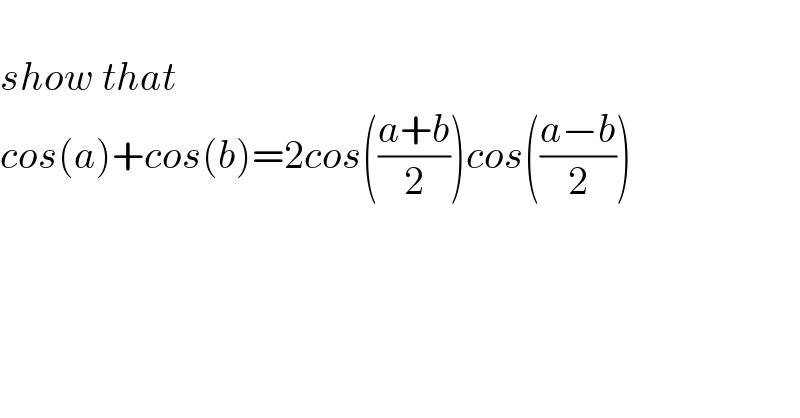
show that cos(a)+cos(b)=2cos(((a+b)/2))cos(((a−b)/2))

$$ \\ $$$${show}\:{that} \\ $$$${cos}\left({a}\right)+{cos}\left({b}\right)=\mathrm{2}{cos}\left(\frac{{a}+{b}}{\mathrm{2}}\right){cos}\left(\frac{{a}−{b}}{\mathrm{2}}\right) \\ $$

Answered by mathmax by abdo last updated on 23/Dec/20

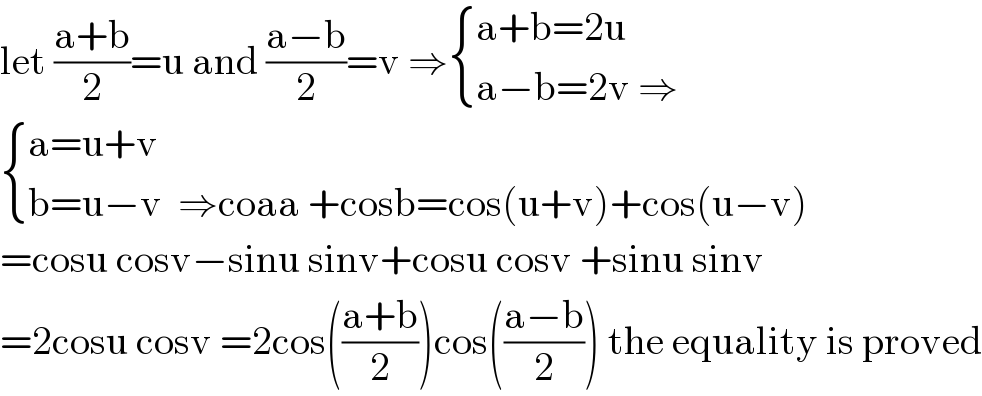
let ((a+b)/2)=u and ((a−b)/2)=v ⇒ { ((a+b=2u)),((a−b=2v ⇒)) :} { ((a=u+v)),((b=u−v ⇒coaa +cosb=cos(u+v)+cos(u−v))) :} =cosu cosv−sinu sinv+cosu cosv +sinu sinv =2cosu cosv =2cos(((a+b)/2))cos(((a−b)/2)) the equality is proved

$$\mathrm{let}\:\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}}=\mathrm{u}\:\mathrm{and}\:\frac{\mathrm{a}−\mathrm{b}}{\mathrm{2}}=\mathrm{v}\:\Rightarrow\begin{cases}{\mathrm{a}+\mathrm{b}=\mathrm{2u}}\\{\mathrm{a}−\mathrm{b}=\mathrm{2v}\:\Rightarrow}\end{cases} \\ $$$$\begin{cases}{\mathrm{a}=\mathrm{u}+\mathrm{v}}\\{\mathrm{b}=\mathrm{u}−\mathrm{v}\:\:\Rightarrow\mathrm{coaa}\:+\mathrm{cosb}=\mathrm{cos}\left(\mathrm{u}+\mathrm{v}\right)+\mathrm{cos}\left(\mathrm{u}−\mathrm{v}\right)}\end{cases} \\ $$$$=\mathrm{cosu}\:\mathrm{cosv}−\mathrm{sinu}\:\mathrm{sinv}+\mathrm{cosu}\:\mathrm{cosv}\:+\mathrm{sinu}\:\mathrm{sinv} \\ $$$$=\mathrm{2cosu}\:\mathrm{cosv}\:=\mathrm{2cos}\left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{a}−\mathrm{b}}{\mathrm{2}}\right)\:\mathrm{the}\:\mathrm{equality}\:\mathrm{is}\:\mathrm{proved} \\ $$

Answered by mr W last updated on 24/Dec/20

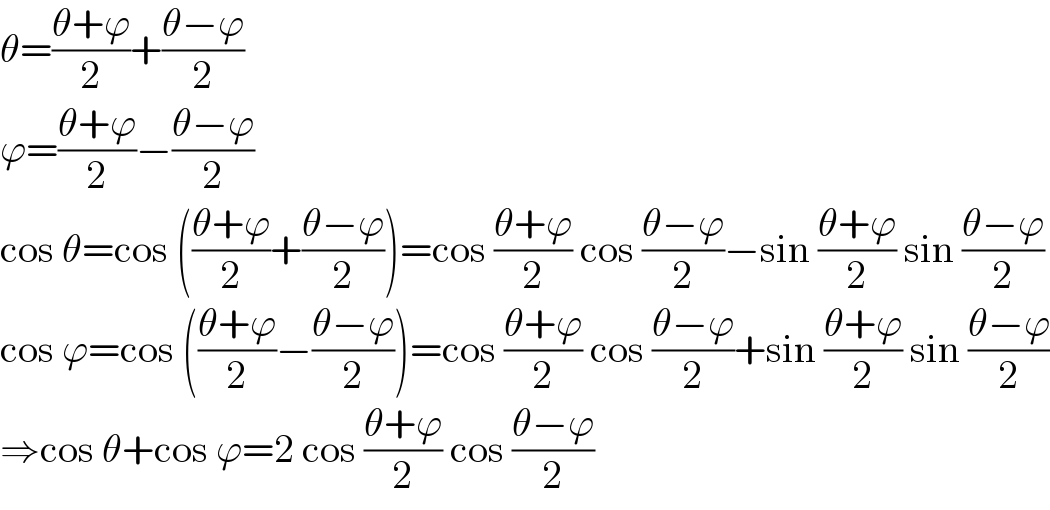
θ=((θ+ϕ)/2)+((θ−ϕ)/2) ϕ=((θ+ϕ)/2)−((θ−ϕ)/2) cos θ=cos (((θ+ϕ)/2)+((θ−ϕ)/2))=cos ((θ+ϕ)/2) cos ((θ−ϕ)/2)−sin ((θ+ϕ)/2) sin ((θ−ϕ)/2) cos ϕ=cos (((θ+ϕ)/2)−((θ−ϕ)/2))=cos ((θ+ϕ)/2) cos ((θ−ϕ)/2)+sin ((θ+ϕ)/2) sin ((θ−ϕ)/2) ⇒cos θ+cos ϕ=2 cos ((θ+ϕ)/2) cos ((θ−ϕ)/2)

$$\theta=\frac{\theta+\varphi}{\mathrm{2}}+\frac{\theta−\varphi}{\mathrm{2}} \\ $$$$\varphi=\frac{\theta+\varphi}{\mathrm{2}}−\frac{\theta−\varphi}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\theta=\mathrm{cos}\:\left(\frac{\theta+\varphi}{\mathrm{2}}+\frac{\theta−\varphi}{\mathrm{2}}\right)=\mathrm{cos}\:\frac{\theta+\varphi}{\mathrm{2}}\:\mathrm{cos}\:\frac{\theta−\varphi}{\mathrm{2}}−\mathrm{sin}\:\frac{\theta+\varphi}{\mathrm{2}}\:\mathrm{sin}\:\frac{\theta−\varphi}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\varphi=\mathrm{cos}\:\left(\frac{\theta+\varphi}{\mathrm{2}}−\frac{\theta−\varphi}{\mathrm{2}}\right)=\mathrm{cos}\:\frac{\theta+\varphi}{\mathrm{2}}\:\mathrm{cos}\:\frac{\theta−\varphi}{\mathrm{2}}+\mathrm{sin}\:\frac{\theta+\varphi}{\mathrm{2}}\:\mathrm{sin}\:\frac{\theta−\varphi}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{cos}\:\theta+\mathrm{cos}\:\varphi=\mathrm{2}\:\mathrm{cos}\:\frac{\theta+\varphi}{\mathrm{2}}\:\mathrm{cos}\:\frac{\theta−\varphi}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com