
Question Number 63300 by Rio Michael last updated on 02/Jul/19
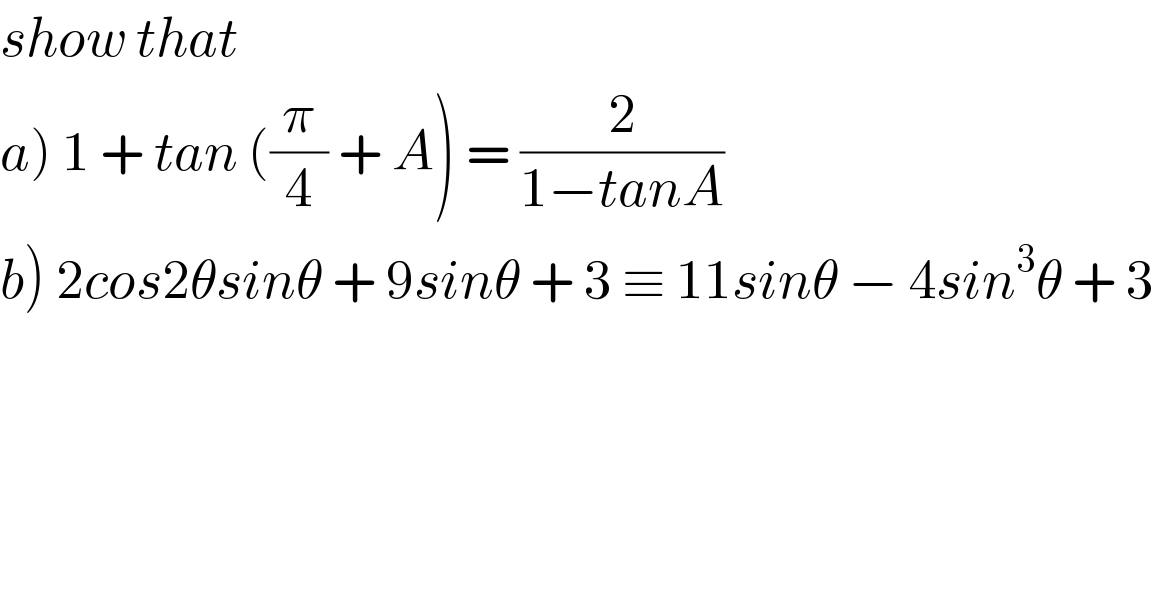
$${show}\:{that}\:\: \\ $$$$\left.{a}\right)\:\mathrm{1}\:+\:{tan}\:\left(\frac{\pi}{\mathrm{4}}\:+\:{A}\right)\:=\:\frac{\mathrm{2}}{\mathrm{1}−{tanA}} \\ $$$$\left.{b}\right)\:\mathrm{2}{cos}\mathrm{2}\theta{sin}\theta\:+\:\mathrm{9}{sin}\theta\:+\:\mathrm{3}\:\equiv\:\mathrm{11}{sin}\theta\:−\:\mathrm{4}{sin}^{\mathrm{3}} \theta\:+\:\mathrm{3} \\ $$
Commented by kaivan.ahmadi last updated on 02/Jul/19
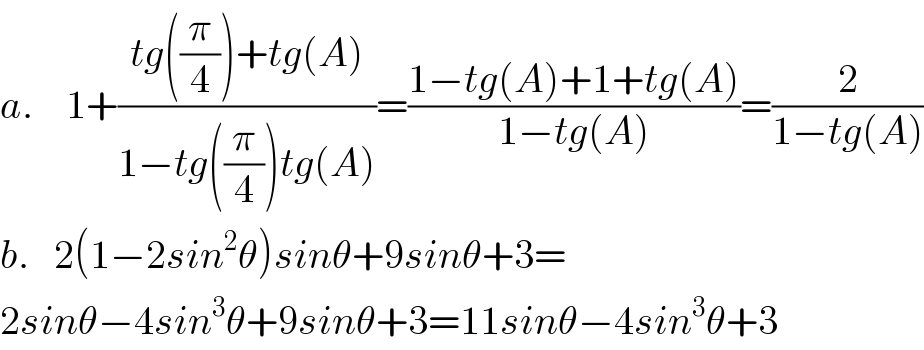
$${a}.\:\:\:\:\mathrm{1}+\frac{{tg}\left(\frac{\pi}{\mathrm{4}}\right)+{tg}\left({A}\right)}{\mathrm{1}−{tg}\left(\frac{\pi}{\mathrm{4}}\right){tg}\left({A}\right)}=\frac{\mathrm{1}−{tg}\left({A}\right)+\mathrm{1}+{tg}\left({A}\right)}{\mathrm{1}−{tg}\left({A}\right)}=\frac{\mathrm{2}}{\mathrm{1}−{tg}\left({A}\right)} \\ $$$${b}.\:\:\:\mathrm{2}\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \theta\right){sin}\theta+\mathrm{9}{sin}\theta+\mathrm{3}= \\ $$$$\mathrm{2}{sin}\theta−\mathrm{4}{sin}^{\mathrm{3}} \theta+\mathrm{9}{sin}\theta+\mathrm{3}=\mathrm{11}{sin}\theta−\mathrm{4}{sin}^{\mathrm{3}} \theta+\mathrm{3} \\ $$
Commented by Rio Michael last updated on 02/Jul/19

$${thats}\:{right} \\ $$
