
Question Number 46569 by scientist last updated on 28/Oct/18
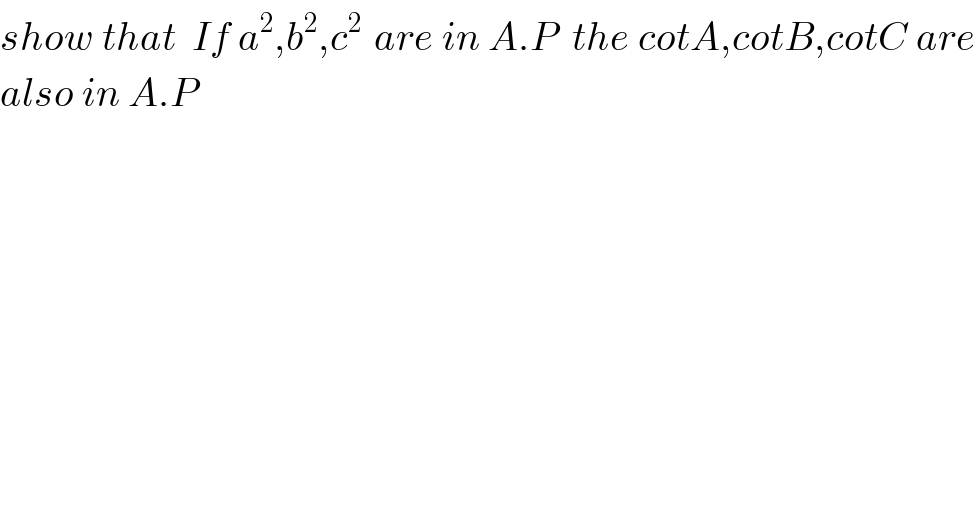
$${show}\:{that}\:\:{If}\:{a}^{\mathrm{2}} ,{b}^{\mathrm{2}} ,{c}^{\mathrm{2}\:} \:{are}\:{in}\:{A}.{P}\:\:{the}\:{cotA},{cotB},{cotC}\:{are} \\ $$$${also}\:{in}\:{A}.{P} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 28/Oct/18
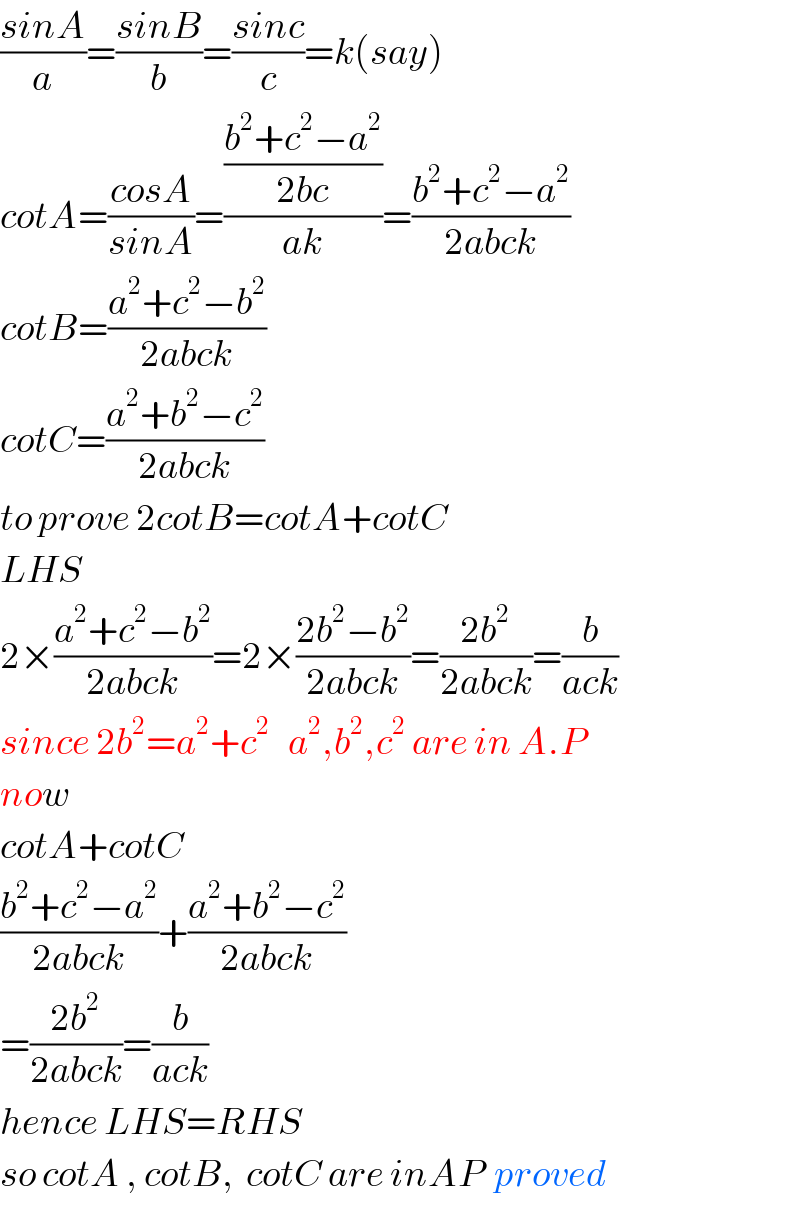
$$\frac{{sinA}}{{a}}=\frac{{sinB}}{{b}}=\frac{{sinc}}{{c}}={k}\left({say}\right) \\ $$$${cotA}=\frac{{cosA}}{{sinA}}=\frac{\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}}{{ak}}=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{abck}} \\ $$$${cotB}=\frac{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{abck}} \\ $$$${cotC}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{abck}} \\ $$$${to}\:{prove}\:\mathrm{2}{cotB}={cotA}+{cotC} \\ $$$${LHS} \\ $$$$\mathrm{2}×\frac{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{abck}}=\mathrm{2}×\frac{\mathrm{2}{b}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{abck}}=\frac{\mathrm{2}{b}^{\mathrm{2}} }{\mathrm{2}{abck}}=\frac{{b}}{{ack}} \\ $$$${since}\:\mathrm{2}{b}^{\mathrm{2}} ={a}^{\mathrm{2}} +{c}^{\mathrm{2}} \:\:\:{a}^{\mathrm{2}} ,{b}^{\mathrm{2}} ,{c}^{\mathrm{2}} \:{are}\:{in}\:{A}.{P} \\ $$$${now} \\ $$$${cotA}+{cotC} \\ $$$$\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{abck}}+\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{abck}} \\ $$$$=\frac{\mathrm{2}{b}^{\mathrm{2}} }{\mathrm{2}{abck}}=\frac{{b}}{{ack}} \\ $$$${hence}\:{LHS}={RHS} \\ $$$${so}\:{cotA}\:,\:{cotB},\:\:{cotC}\:{are}\:{inAP}\:\:{proved} \\ $$
