Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 198423 by pascal889 last updated on 19/Oct/23

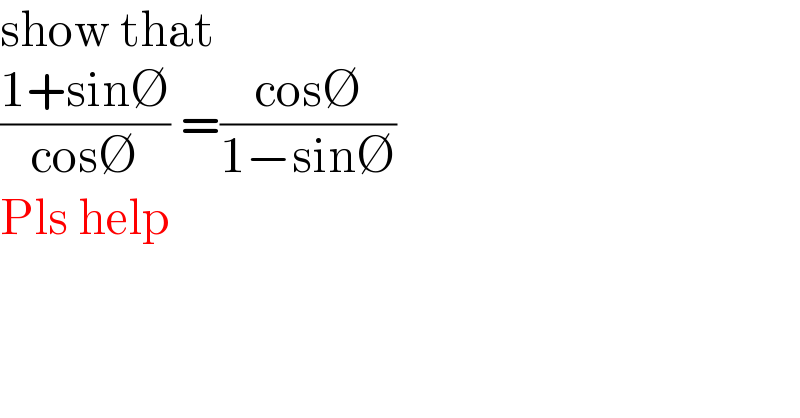
show that ((1+sin∅)/(cos∅)) =((cos∅)/(1−sin∅)) Pls help

$$\mathrm{show}\:\mathrm{that} \\ $$$$\frac{\mathrm{1}+\mathrm{sin}\varnothing}{\mathrm{cos}\varnothing}\:=\frac{\mathrm{cos}\varnothing}{\mathrm{1}−\mathrm{sin}\varnothing} \\ $$$$\mathrm{Pls}\:\mathrm{help} \\ $$$$ \\ $$

Answered by BaliramKumar last updated on 19/Oct/23

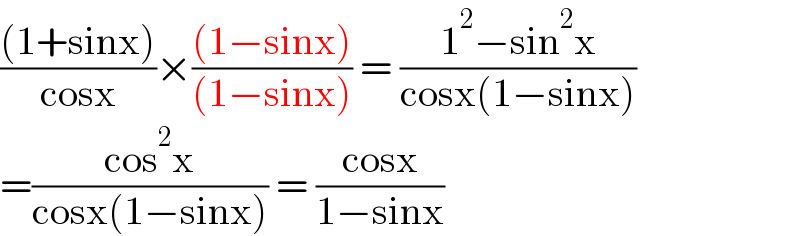
(((1+sinx))/(cosx))×(((1−sinx))/((1−sinx))) = ((1^2 −sin^2 x)/(cosx(1−sinx))) =((cos^2 x)/(cosx(1−sinx))) = ((cosx)/(1−sinx))

$$\frac{\left(\mathrm{1}+\mathrm{sinx}\right)}{\mathrm{cosx}}×\frac{\left(\mathrm{1}−\mathrm{sinx}\right)}{\left(\mathrm{1}−\mathrm{sinx}\right)}\:=\:\frac{\mathrm{1}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{cosx}\left(\mathrm{1}−\mathrm{sinx}\right)} \\ $$$$=\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{cosx}\left(\mathrm{1}−\mathrm{sinx}\right)}\:=\:\frac{\mathrm{cosx}}{\mathrm{1}−\mathrm{sinx}} \\ $$

Answered by Rasheed.Sindhi last updated on 19/Oct/23

sin^2 θ+cos^2 θ=1 [An identity that we know] ⇒1−sin^2 θ=cos^2 θ ⇒(1−sinθ)(1+sinθ)=(cosθ)(cosθ) ⇒((1+sinθ)/(cosθ )) =((cosθ )/(1−sinθ))

$$\:\:\mathrm{sin}^{\mathrm{2}} \theta+\mathrm{cos}^{\mathrm{2}} \theta=\mathrm{1}\:\:\left[{An}\:{identity}\:{that}\:{we}\:{know}\right] \\ $$$$\:\:\Rightarrow\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta=\mathrm{cos}^{\mathrm{2}} \theta \\ $$$$\:\:\Rightarrow\left(\mathrm{1}−\mathrm{sin}\theta\right)\left(\mathrm{1}+\mathrm{sin}\theta\right)=\left(\mathrm{cos}\theta\right)\left(\mathrm{cos}\theta\right) \\ $$$$\:\:\Rightarrow\frac{\mathrm{1}+\mathrm{sin}\theta}{\mathrm{cos}\theta\:}\:=\frac{\mathrm{cos}\theta\:}{\mathrm{1}−\mathrm{sin}\theta}\:\:\:\:\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com