Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 187330 by Humble last updated on 16/Feb/23

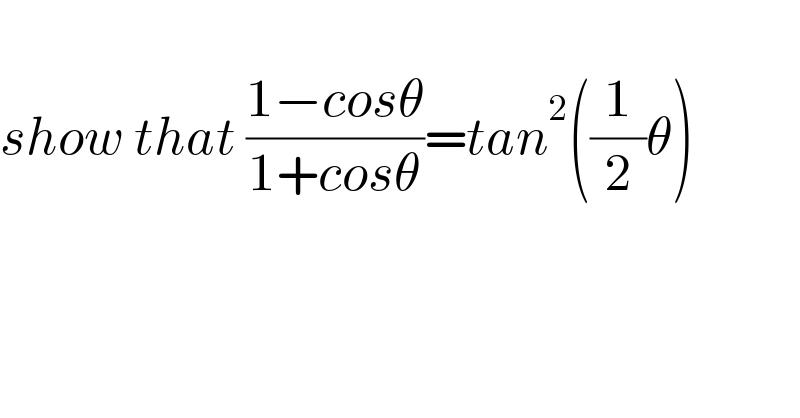
show that ((1−cosθ)/(1+cosθ))=tan^2 ((1/2)θ)

$$ \\ $$$${show}\:{that}\:\frac{\mathrm{1}−{cos}\theta}{\mathrm{1}+{cos}\theta}={tan}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\theta\right)\:\:\: \\ $$

Answered by Frix last updated on 16/Feb/23

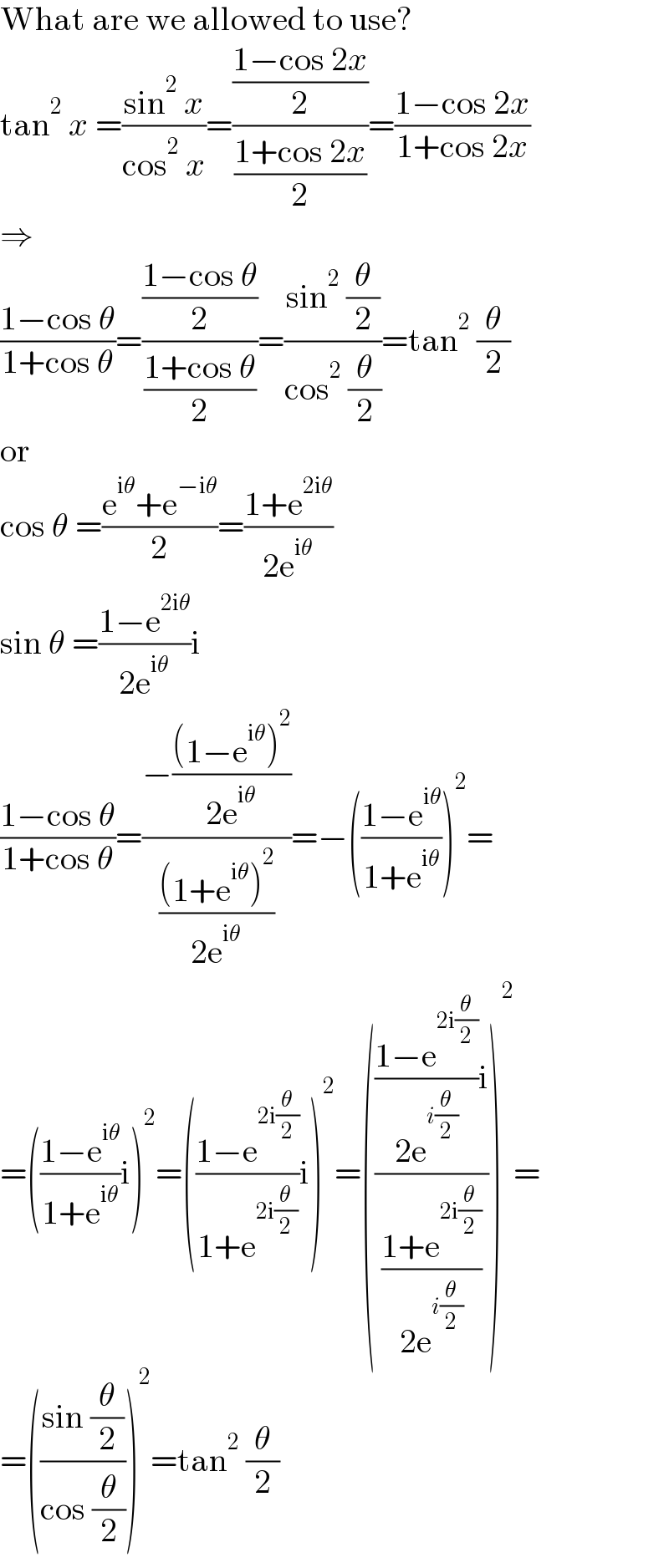
What are we allowed to use? tan^2 x =((sin^2 x)/(cos^2 x))=(((1−cos 2x)/2)/((1+cos 2x)/2))=((1−cos 2x)/(1+cos 2x)) ⇒ ((1−cos θ)/(1+cos θ))=(((1−cos θ)/2)/((1+cos θ)/2))=((sin^2 (θ/2))/(cos^2 (θ/2)))=tan^2 (θ/2) or cos θ =((e^(iθ) +e^(−iθ) )/2)=((1+e^(2iθ) )/(2e^(iθ) )) sin θ =((1−e^(2iθ) )/(2e^(iθ) ))i ((1−cos θ)/(1+cos θ))=((−(((1−e^(iθ) )^2 )/(2e^(iθ) )))/(((1+e^(iθ) )^2 )/(2e^(iθ) )))=−(((1−e^(iθ) )/(1+e^(iθ) )))^2 = =(((1−e^(iθ) )/(1+e^(iθ) ))i)^2 =(((1−e^(2i(θ/2)) )/(1+e^(2i(θ/2)) ))i)^2 =(((((1−e^(2i(θ/2)) )/(2e^(i(θ/2)) ))i)/((1+e^(2i(θ/2)) )/(2e^(i(θ/2)) ))))^2 = =(((sin (θ/2))/(cos (θ/2))))^2 =tan^2 (θ/2)

$$\mathrm{What}\:\mathrm{are}\:\mathrm{we}\:\mathrm{allowed}\:\mathrm{to}\:\mathrm{use}? \\ $$$$\mathrm{tan}^{\mathrm{2}} \:{x}\:=\frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{\mathrm{cos}^{\mathrm{2}} \:{x}}=\frac{\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}}}{\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}}}=\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}} \\ $$$$\Rightarrow \\ $$$$\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\mathrm{1}+\mathrm{cos}\:\theta}=\frac{\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\mathrm{2}}}{\frac{\mathrm{1}+\mathrm{cos}\:\theta}{\mathrm{2}}}=\frac{\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}{\mathrm{cos}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}=\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{or} \\ $$$$\mathrm{cos}\:\theta\:=\frac{\mathrm{e}^{\mathrm{i}\theta} +\mathrm{e}^{−\mathrm{i}\theta} }{\mathrm{2}}=\frac{\mathrm{1}+\mathrm{e}^{\mathrm{2i}\theta} }{\mathrm{2e}^{\mathrm{i}\theta} } \\ $$$$\mathrm{sin}\:\theta\:=\frac{\mathrm{1}−\mathrm{e}^{\mathrm{2i}\theta} }{\mathrm{2e}^{\mathrm{i}\theta} }\mathrm{i} \\ $$$$\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\mathrm{1}+\mathrm{cos}\:\theta}=\frac{−\frac{\left(\mathrm{1}−\mathrm{e}^{\mathrm{i}\theta} \right)^{\mathrm{2}} }{\mathrm{2e}^{\mathrm{i}\theta} }}{\frac{\left(\mathrm{1}+\mathrm{e}^{\mathrm{i}\theta} \right)^{\mathrm{2}} }{\mathrm{2e}^{\mathrm{i}\theta} }}=−\left(\frac{\mathrm{1}−\mathrm{e}^{\mathrm{i}\theta} }{\mathrm{1}+\mathrm{e}^{\mathrm{i}\theta} }\right)^{\mathrm{2}} = \\ $$$$=\left(\frac{\mathrm{1}−\mathrm{e}^{\mathrm{i}\theta} }{\mathrm{1}+\mathrm{e}^{\mathrm{i}\theta} }\mathrm{i}\right)^{\mathrm{2}} =\left(\frac{\mathrm{1}−\mathrm{e}^{\mathrm{2i}\frac{\theta}{\mathrm{2}}} }{\mathrm{1}+\mathrm{e}^{\mathrm{2i}\frac{\theta}{\mathrm{2}}} }\mathrm{i}\right)^{\mathrm{2}} =\left(\frac{\frac{\mathrm{1}−\mathrm{e}^{\mathrm{2i}\frac{\theta}{\mathrm{2}}} }{\mathrm{2e}^{{i}\frac{\theta}{\mathrm{2}}} }\mathrm{i}}{\frac{\mathrm{1}+\mathrm{e}^{\mathrm{2i}\frac{\theta}{\mathrm{2}}} }{\mathrm{2e}^{{i}\frac{\theta}{\mathrm{2}}} }}\right)^{\mathrm{2}} = \\ $$$$=\left(\frac{\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}{\mathrm{cos}\:\frac{\theta}{\mathrm{2}}}\right)^{\mathrm{2}} =\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}} \\ $$

Commented by Humble last updated on 16/Feb/23

awesome!!. thank you, sir

$${awesome}!!.\:{thank}\:{you},\:{sir} \\ $$

Commented by Frix last updated on 16/Feb/23

��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com