
Question Number 210839 by klipto last updated on 19/Aug/24
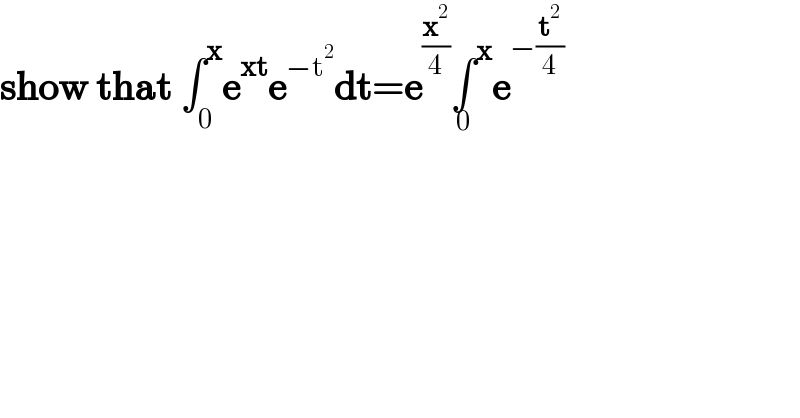
$$\boldsymbol{\mathrm{show}}\:\boldsymbol{\mathrm{that}}\:\int_{\mathrm{0}} ^{\boldsymbol{\mathrm{x}}} \boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{xt}}} \boldsymbol{\mathrm{e}}^{−\mathrm{t}^{\mathrm{2}} } \boldsymbol{\mathrm{dt}}=\boldsymbol{\mathrm{e}}^{\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\mathrm{4}}} \underset{\mathrm{0}} {\int}^{\boldsymbol{\mathrm{x}}} \boldsymbol{\mathrm{e}}^{−\frac{\boldsymbol{\mathrm{t}}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$ \\ $$
Commented by Frix last updated on 20/Aug/24
![∫_0 ^x e^(xt) e^(−t^2 ) dt= [u=2t−x] =(e^(x^2 /4) /2)∫_(−x) ^x e^(−(u^2 /4)) du= =e^(x^2 /4) ∫_0 ^x e^(−(u^2 /4)) du](Q210847.png)
$$\underset{\mathrm{0}} {\overset{{x}} {\int}}\mathrm{e}^{{xt}} \mathrm{e}^{−{t}^{\mathrm{2}} } {dt}=\:\:\:\:\:\left[{u}=\mathrm{2}{t}−{x}\right] \\ $$$$=\frac{\mathrm{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}} }{\mathrm{2}}\underset{−{x}} {\overset{{x}} {\int}}\mathrm{e}^{−\frac{{u}^{\mathrm{2}} }{\mathrm{4}}} {du}= \\ $$$$=\mathrm{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}} \underset{\mathrm{0}} {\overset{{x}} {\int}}\mathrm{e}^{−\frac{{u}^{\mathrm{2}} }{\mathrm{4}}} {du} \\ $$
