
Question Number 201829 by 281981 last updated on 13/Dec/23
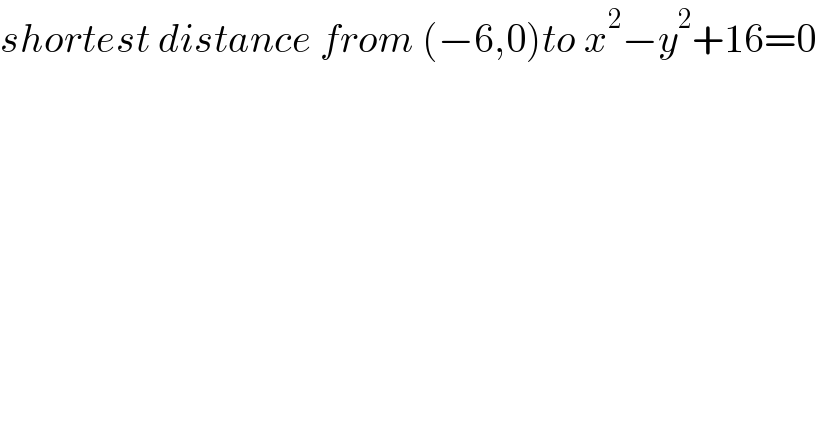
$${shortest}\:{distance}\:{from}\:\left(−\mathrm{6},\mathrm{0}\right){to}\:{x}^{\mathrm{2}} −{y}^{\mathrm{2}} +\mathrm{16}=\mathrm{0} \\ $$
Answered by esmaeil last updated on 13/Dec/23
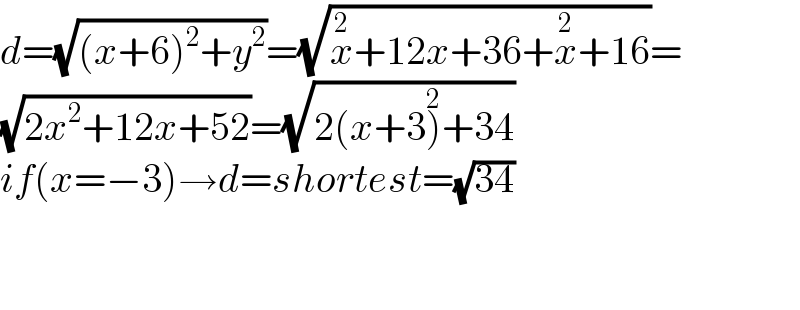
$${d}=\sqrt{\left({x}+\mathrm{6}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }=\sqrt{\overset{\mathrm{2}} {{x}}+\mathrm{12}{x}+\mathrm{36}+\overset{\mathrm{2}} {{x}}+\mathrm{16}}= \\ $$$$\sqrt{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{12}{x}+\mathrm{52}}=\sqrt{\mathrm{2}\left({x}+\mathrm{3}\overset{\mathrm{2}} {\right)}+\mathrm{34}} \\ $$$${if}\left({x}=−\mathrm{3}\right)\rightarrow{d}={shortest}=\sqrt{\mathrm{34}} \\ $$$$ \\ $$$$ \\ $$
Commented by 281981 last updated on 14/Dec/23

$${tnq}\:{sir} \\ $$
Answered by mr W last updated on 13/Dec/23
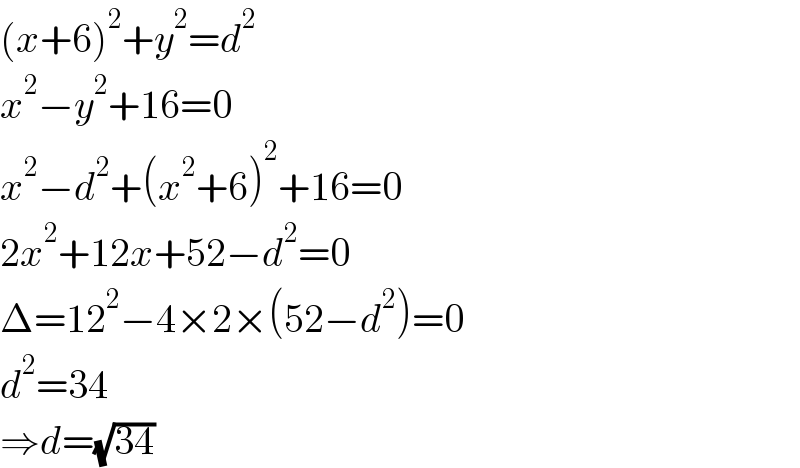
$$\left({x}+\mathrm{6}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={d}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} +\mathrm{16}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{d}^{\mathrm{2}} +\left({x}^{\mathrm{2}} +\mathrm{6}\right)^{\mathrm{2}} +\mathrm{16}=\mathrm{0} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{12}{x}+\mathrm{52}−{d}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Delta=\mathrm{12}^{\mathrm{2}} −\mathrm{4}×\mathrm{2}×\left(\mathrm{52}−{d}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${d}^{\mathrm{2}} =\mathrm{34} \\ $$$$\Rightarrow{d}=\sqrt{\mathrm{34}} \\ $$
Commented by 281981 last updated on 14/Dec/23

$${tnq}\:{sir} \\ $$
