Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 100771 by Rio Michael last updated on 28/Jun/20

sho that (0,(1/2)) is a point of symetry for the curve f(x) = x +(1/(1−e^x )) Please make a reference to a book i can understand centre of symmetry of rational functions and functions like this

$$\:\mathrm{sho}\:\mathrm{that}\:\:\left(\mathrm{0},\frac{\mathrm{1}}{\mathrm{2}}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{point}\:\mathrm{of}\:\mathrm{symetry}\:\mathrm{for}\:\mathrm{the}\:\mathrm{curve} \\ $$$$\:{f}\left({x}\right)\:=\:{x}\:+\frac{\mathrm{1}}{\mathrm{1}−{e}^{{x}} } \\ $$$$\mathrm{Please}\:\mathrm{make}\:\mathrm{a}\:\mathrm{reference}\:\mathrm{to}\:\mathrm{a}\:\mathrm{book}\:\mathrm{i}\:\mathrm{can}\:\mathrm{understand} \\ $$$$\mathrm{centre}\:\mathrm{of}\:\mathrm{symmetry}\:\mathrm{of}\:\mathrm{rational}\:\mathrm{functions}\:\mathrm{and}\:\mathrm{functions} \\ $$$$\mathrm{like}\:\mathrm{this} \\ $$

Commented by abdomathmax last updated on 28/Jun/20

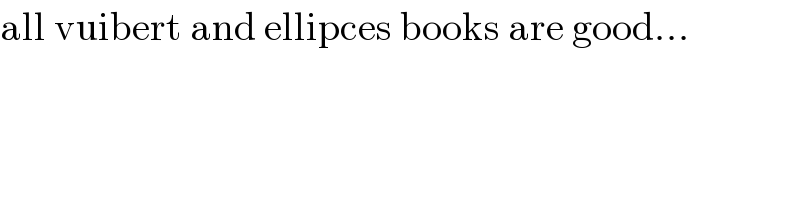
all vuibert and ellipces books are good...

$$\mathrm{all}\:\mathrm{vuibert}\:\mathrm{and}\:\mathrm{ellipces}\:\mathrm{books}\:\mathrm{are}\:\mathrm{good}... \\ $$

Answered by MJS last updated on 28/Jun/20

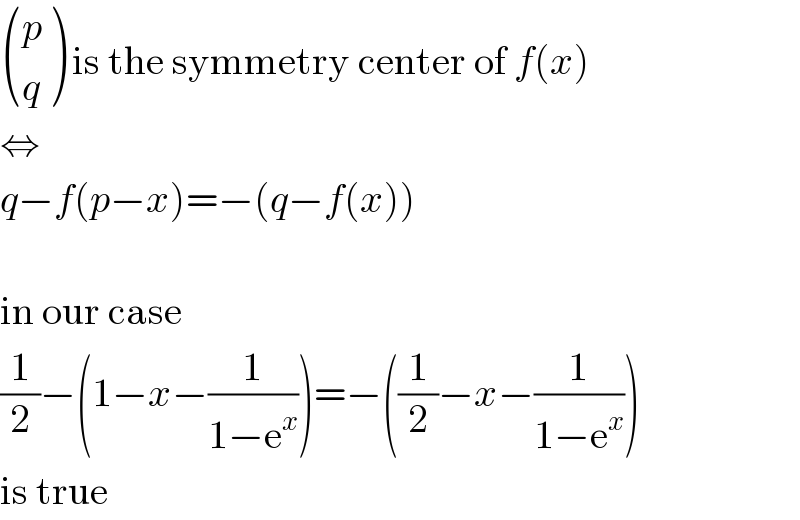
((p),(q) ) is the symmetry center of f(x) ⇔ q−f(p−x)=−(q−f(x)) in our case (1/2)−(1−x−(1/(1−e^x )))=−((1/2)−x−(1/(1−e^x ))) is true

$$\begin{pmatrix}{{p}}\\{{q}}\end{pmatrix}\:\mathrm{is}\:\mathrm{the}\:\mathrm{symmetry}\:\mathrm{center}\:\mathrm{of}\:{f}\left({x}\right) \\ $$$$\Leftrightarrow \\ $$$${q}−{f}\left({p}−{x}\right)=−\left({q}−{f}\left({x}\right)\right) \\ $$$$ \\ $$$$\mathrm{in}\:\mathrm{our}\:\mathrm{case} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}−\left(\mathrm{1}−{x}−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{e}^{{x}} }\right)=−\left(\frac{\mathrm{1}}{\mathrm{2}}−{x}−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{e}^{{x}} }\right) \\ $$$$\mathrm{is}\:\mathrm{true} \\ $$

Commented by MJS last updated on 28/Jun/20

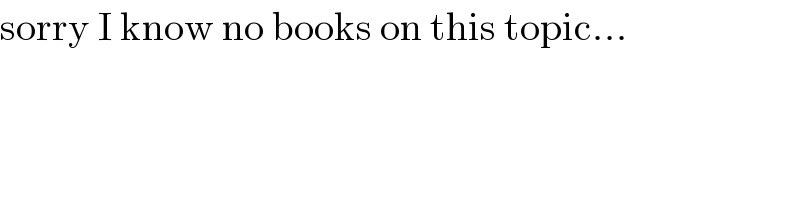
sorry I know no books on this topic...

$$\mathrm{sorry}\:\mathrm{I}\:\mathrm{know}\:\mathrm{no}\:\mathrm{books}\:\mathrm{on}\:\mathrm{this}\:\mathrm{topic}... \\ $$

Answered by abdomathmax last updated on 28/Jun/20

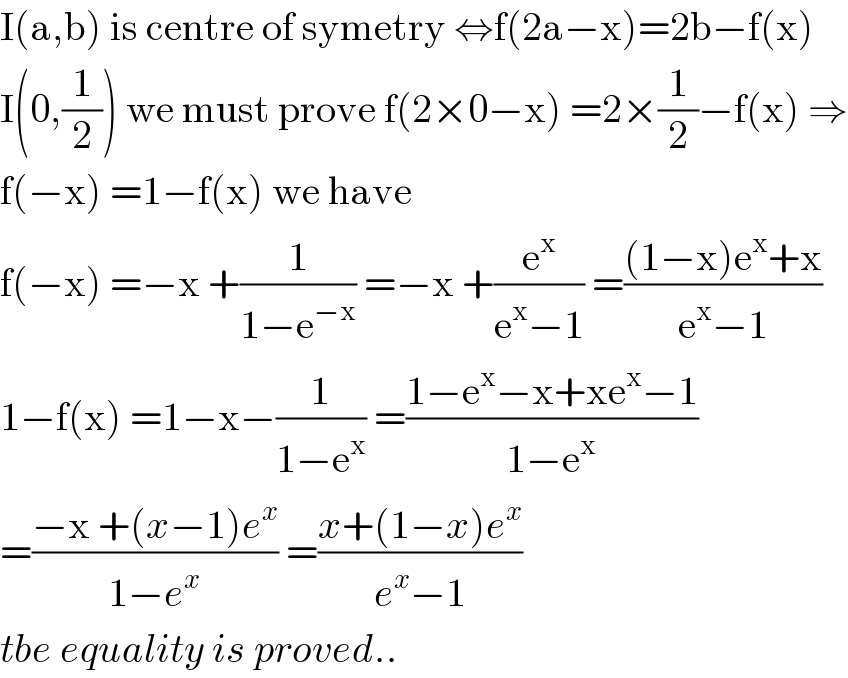
I(a,b) is centre of symetry ⇔f(2a−x)=2b−f(x) I(0,(1/2)) we must prove f(2×0−x) =2×(1/2)−f(x) ⇒ f(−x) =1−f(x) we have f(−x) =−x +(1/(1−e^(−x) )) =−x +(e^x /(e^x −1)) =(((1−x)e^x +x)/(e^x −1)) 1−f(x) =1−x−(1/(1−e^x )) =((1−e^x −x+xe^x −1)/(1−e^x )) =((−x +(x−1)e^x )/(1−e^x )) =((x+(1−x)e^x )/(e^x −1)) tbe equality is proved..

$$\mathrm{I}\left(\mathrm{a},\mathrm{b}\right)\:\mathrm{is}\:\mathrm{centre}\:\mathrm{of}\:\mathrm{symetry}\:\Leftrightarrow\mathrm{f}\left(\mathrm{2a}−\mathrm{x}\right)=\mathrm{2b}−\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\mathrm{I}\left(\mathrm{0},\frac{\mathrm{1}}{\mathrm{2}}\right)\:\mathrm{we}\:\mathrm{must}\:\mathrm{prove}\:\mathrm{f}\left(\mathrm{2}×\mathrm{0}−\mathrm{x}\right)\:=\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{f}\left(\mathrm{x}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(−\mathrm{x}\right)\:=\mathrm{1}−\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{f}\left(−\mathrm{x}\right)\:=−\mathrm{x}\:+\frac{\mathrm{1}}{\mathrm{1}−\mathrm{e}^{−\mathrm{x}} }\:=−\mathrm{x}\:+\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}\:=\frac{\left(\mathrm{1}−\mathrm{x}\right)\mathrm{e}^{\mathrm{x}} +\mathrm{x}}{\mathrm{e}^{\mathrm{x}} −\mathrm{1}} \\ $$$$\mathrm{1}−\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{1}−\mathrm{x}−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{e}^{\mathrm{x}} }\:=\frac{\mathrm{1}−\mathrm{e}^{\mathrm{x}} −\mathrm{x}+\mathrm{xe}^{\mathrm{x}} −\mathrm{1}}{\mathrm{1}−\mathrm{e}^{\mathrm{x}} } \\ $$$$=\frac{−\mathrm{x}\:+\left({x}−\mathrm{1}\right){e}^{{x}} }{\mathrm{1}−{e}^{{x}} }\:=\frac{{x}+\left(\mathrm{1}−{x}\right){e}^{{x}} }{{e}^{{x}} −\mathrm{1}} \\ $$$${tbe}\:{equality}\:{is}\:{proved}.. \\ $$

Commented by Rio Michael last updated on 28/Jun/20

thank you all

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{all} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com