Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 187408 by MathsFan last updated on 17/Feb/23

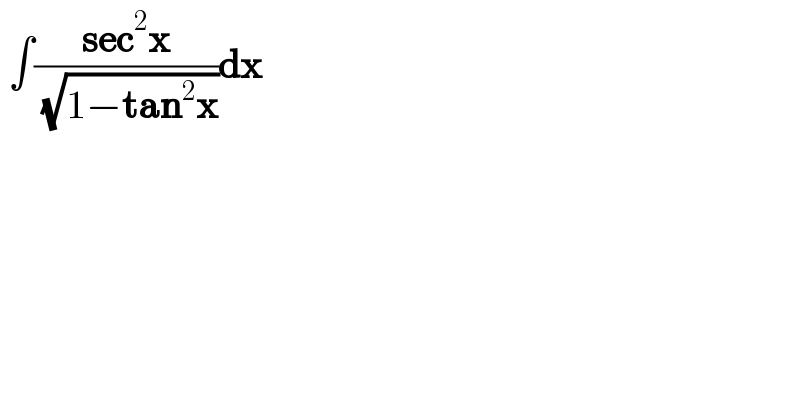
∫((sec^2 x)/( (√(1−tan^2 x))))dx

$$\:\int\frac{\boldsymbol{\mathrm{sec}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}}{\:\sqrt{\mathrm{1}−\boldsymbol{\mathrm{tan}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}}}\boldsymbol{\mathrm{dx}} \\ $$

Answered by horsebrand11 last updated on 17/Feb/23

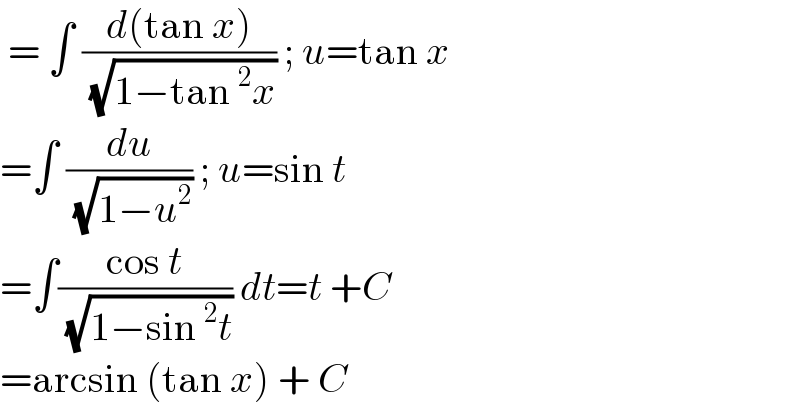
= ∫ ((d(tan x))/( (√(1−tan^2 x)))) ; u=tan x =∫ (du/( (√(1−u^2 )))) ; u=sin t =∫((cos t)/( (√(1−sin^2 t)))) dt=t +C =arcsin (tan x) + C

$$\:=\:\int\:\frac{{d}\left(\mathrm{tan}\:{x}\right)}{\:\sqrt{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} {x}}}\:;\:{u}=\mathrm{tan}\:{x} \\ $$$$=\int\:\frac{{du}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}\:;\:{u}=\mathrm{sin}\:{t} \\ $$$$=\int\frac{\mathrm{cos}\:{t}}{\:\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {t}}}\:{dt}={t}\:+{C} \\ $$$$=\mathrm{arcsin}\:\left(\mathrm{tan}\:{x}\right)\:+\:{C} \\ $$

Commented by MJS_new last updated on 17/Feb/23

arcsin tan x check it!

$$\mathrm{arcsin}\:\mathrm{tan}\:{x} \\ $$$$\mathrm{check}\:\mathrm{it}! \\ $$

Commented by horsebrand11 last updated on 17/Feb/23

yes thanks

$${yes}\:{thanks} \\ $$

Answered by MJS_new last updated on 17/Feb/23

I love complicated paths ∫((sec^2 x)/( (√(1−tan^2 x))))dx=∫(dx/(cos x (√(1−2sin^2 x))))= [t=(((√2)sin x)/( (√(1−2sin^2 x)))) → dx=(((1−2sin^2 x)^(3/2) )/( (√2)cos x))] =(√2)∫(dt/(t^2 +2))=arctan (t/( (√2))) = =arctan ((sin x)/( (√(1−2sin^2 x)))) =arcsin tan x +C

$$\mathrm{I}\:\mathrm{love}\:\mathrm{complicated}\:\mathrm{paths} \\ $$$$\int\frac{\mathrm{sec}^{\mathrm{2}} \:{x}}{\:\sqrt{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:{x}}}{dx}=\int\frac{{dx}}{\mathrm{cos}\:{x}\:\sqrt{\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:{x}}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{\mathrm{2}}\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:{x}}}\:\rightarrow\:{dx}=\frac{\left(\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:{x}\right)^{\mathrm{3}/\mathrm{2}} }{\:\sqrt{\mathrm{2}}\mathrm{cos}\:{x}}\right] \\ $$$$=\sqrt{\mathrm{2}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{2}}=\mathrm{arctan}\:\frac{{t}}{\:\sqrt{\mathrm{2}}}\:= \\ $$$$=\mathrm{arctan}\:\frac{\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:{x}}}\:=\mathrm{arcsin}\:\mathrm{tan}\:{x}\:+{C} \\ $$

Commented by MathsFan last updated on 17/Feb/23

thank you sir i appreciate your effort

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$$$\mathrm{i}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com