Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 102115 by Dwaipayan Shikari last updated on 06/Jul/20

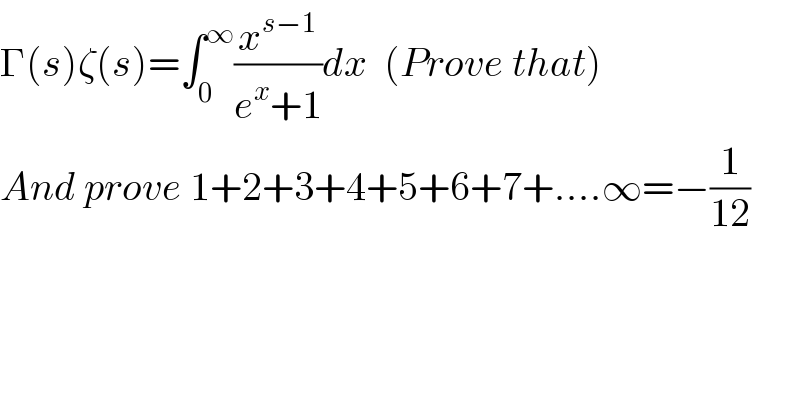
Γ(s)ζ(s)=∫_0 ^∞ (x^(s−1) /(e^x +1))dx (Prove that) And prove 1+2+3+4+5+6+7+....∞=−(1/(12))

$$\Gamma\left({s}\right)\zeta\left({s}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{s}−\mathrm{1}} }{{e}^{{x}} +\mathrm{1}}{dx}\:\:\left({Prove}\:{that}\right) \\ $$$${And}\:{prove}\:\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{7}+....\infty=−\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$ \\ $$

Commented by mr W last updated on 06/Jul/20

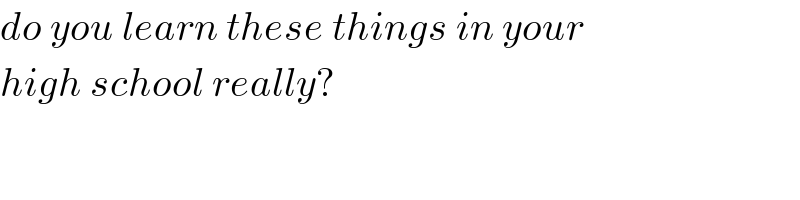
do you learn these things in your high school really?

$${do}\:{you}\:{learn}\:{these}\:{things}\:{in}\:{your} \\ $$$${high}\:{school}\:{really}? \\ $$

Commented by prakash jain last updated on 07/Jul/20

The second question 1+2+3+4+...=−(1/(12)) is proved using analytical comtinuity. Search forum for analytical continuity to get same question answered earlier.

$$\mathrm{The}\:\mathrm{second}\:\mathrm{question}\: \\ $$$$\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+...=−\frac{\mathrm{1}}{\mathrm{12}}\:\mathrm{is}\:\mathrm{proved}\:\mathrm{using} \\ $$$$\mathrm{analytical}\:\mathrm{comtinuity}.\:\mathrm{Search}\:\mathrm{forum} \\ $$$$\mathrm{for}\:\mathrm{analytical}\:\mathrm{continuity}\:\mathrm{to}\:\mathrm{get} \\ $$$$\mathrm{same}\:\mathrm{question}\:\mathrm{answered}\:\mathrm{earlier}. \\ $$

Commented by Dwaipayan Shikari last updated on 07/Jul/20

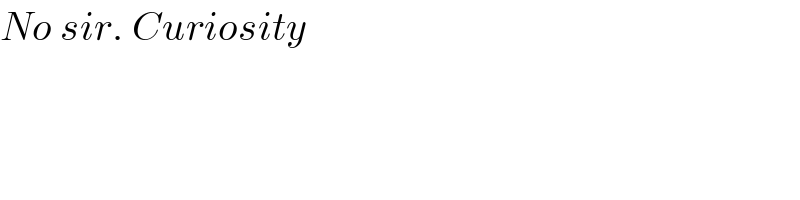
No sir. Curiosity

$${No}\:{sir}.\:{Curiosity} \\ $$

Answered by mathmax by abdo last updated on 06/Jul/20

the question (1)is done see the platform

$$\mathrm{the}\:\:\mathrm{question}\:\left(\mathrm{1}\right)\mathrm{is}\:\mathrm{done}\:\mathrm{see}\:\mathrm{the}\:\mathrm{platform} \\ $$

Answered by mathmax by abdo last updated on 08/Jul/20

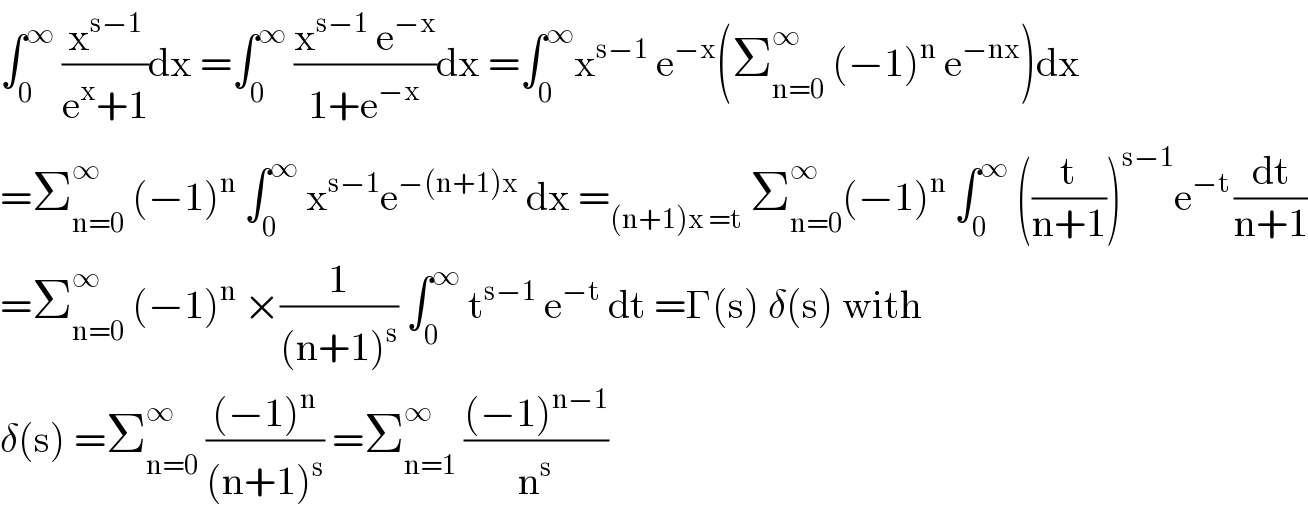
∫_0 ^∞ (x^(s−1) /(e^x +1))dx =∫_0 ^∞ ((x^(s−1) e^(−x) )/(1+e^(−x) ))dx =∫_0 ^∞ x^(s−1) e^(−x) (Σ_(n=0) ^∞ (−1)^n e^(−nx) )dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ x^(s−1) e^(−(n+1)x) dx =_((n+1)x =t) Σ_(n=0) ^(∞ ) (−1)^n ∫_0 ^∞ ((t/(n+1)))^(s−1) e^(−t ) (dt/(n+1)) =Σ_(n=0) ^∞ (−1)^n ×(1/((n+1)^s )) ∫_0 ^∞ t^(s−1) e^(−t) dt =Γ(s) δ(s) with δ(s) =Σ_(n=0) ^∞ (((−1)^n )/((n+1)^s )) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n^s )

$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{s}−\mathrm{1}} }{\mathrm{e}^{\mathrm{x}} +\mathrm{1}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{s}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{x}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{s}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{x}} \left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{nx}} \right)\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{s}−\mathrm{1}} \mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}} \:\mathrm{dx}\:=_{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}\:=\mathrm{t}} \:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty\:} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{t}}{\mathrm{n}+\mathrm{1}}\right)^{\mathrm{s}−\mathrm{1}} \mathrm{e}^{−\mathrm{t}\:} \frac{\mathrm{dt}}{\mathrm{n}+\mathrm{1}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:×\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{s}} }\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{s}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:=\Gamma\left(\mathrm{s}\right)\:\delta\left(\mathrm{s}\right)\:\mathrm{with} \\ $$$$\delta\left(\mathrm{s}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{s}} }\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{s}} } \\ $$

Answered by mathmax by abdo last updated on 08/Jul/20

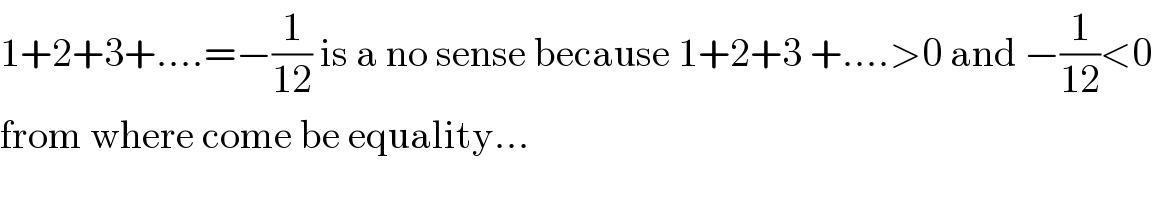
1+2+3+....=−(1/(12)) is a no sense because 1+2+3 +....>0 and −(1/(12))<0 from where come be equality...

$$\mathrm{1}+\mathrm{2}+\mathrm{3}+....=−\frac{\mathrm{1}}{\mathrm{12}}\:\mathrm{is}\:\mathrm{a}\:\mathrm{no}\:\mathrm{sense}\:\mathrm{because}\:\mathrm{1}+\mathrm{2}+\mathrm{3}\:+....>\mathrm{0}\:\mathrm{and}\:−\frac{\mathrm{1}}{\mathrm{12}}<\mathrm{0} \\ $$$$\mathrm{from}\:\mathrm{where}\:\mathrm{come}\:\mathrm{be}\:\mathrm{equality}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com