
Question Number 120122 by Khalmohmmad last updated on 29/Oct/20
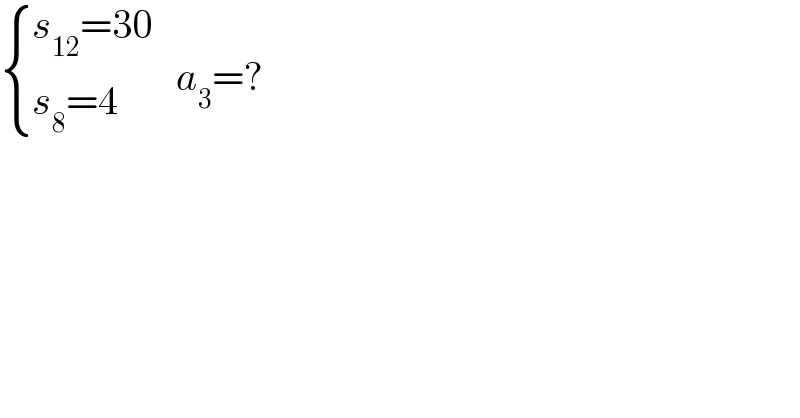
$$\begin{cases}{{s}_{\mathrm{12}} =\mathrm{30}}\\{{s}_{\mathrm{8}} =\mathrm{4}}\end{cases}\:\:\:{a}_{\mathrm{3}} =? \\ $$
Commented by Dwaipayan Shikari last updated on 29/Oct/20

$${a}_{\mathrm{3}} =−\mathrm{1} \\ $$
Commented by Khalmohmmad last updated on 29/Oct/20
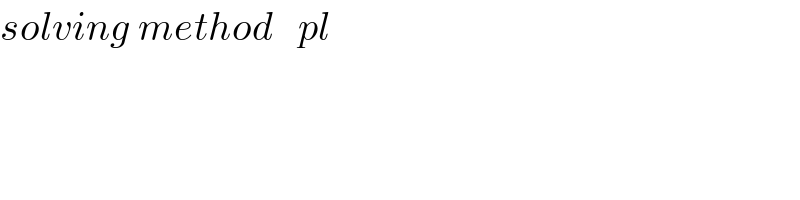
$${solving}\:{method}\:\:\:{pl} \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 29/Oct/20
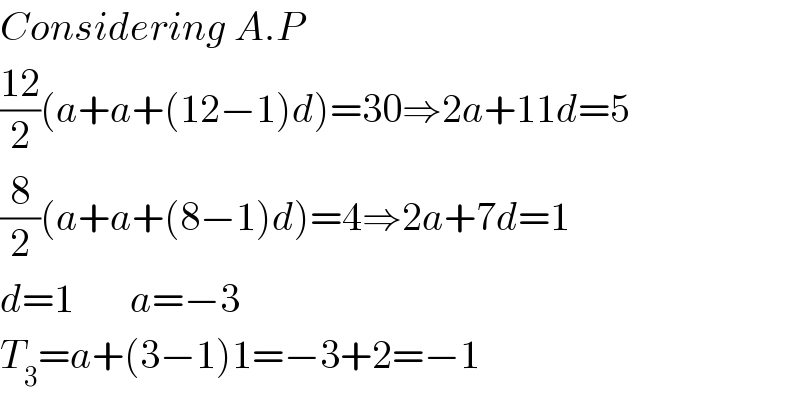
$${Considering}\:{A}.{P} \\ $$$$\frac{\mathrm{12}}{\mathrm{2}}\left({a}+{a}+\left(\mathrm{12}−\mathrm{1}\right){d}\right)=\mathrm{30}\Rightarrow\mathrm{2}{a}+\mathrm{11}{d}=\mathrm{5} \\ $$$$\frac{\mathrm{8}}{\mathrm{2}}\left({a}+{a}+\left(\mathrm{8}−\mathrm{1}\right){d}\right)=\mathrm{4}\Rightarrow\mathrm{2}{a}+\mathrm{7}{d}=\mathrm{1} \\ $$$${d}=\mathrm{1}\:\:\:\:\:\:\:{a}=−\mathrm{3} \\ $$$${T}_{\mathrm{3}} ={a}+\left(\mathrm{3}−\mathrm{1}\right)\mathrm{1}=−\mathrm{3}+\mathrm{2}=−\mathrm{1} \\ $$
