
Question Number 129018 by BHOOPENDRA last updated on 12/Jan/21

$$\frac{\left(\sqrt{{s}}−\mathrm{1}\right)^{\mathrm{2}} }{{s}^{\mathrm{2}} }\:{find}\:{the}\:{inverse}\:{laplace}\:{transformtion} \\ $$
Answered by Dwaipayan Shikari last updated on 12/Jan/21
![L^(−1) ((1/s)−(2/( s^(3/2) ))+(1/s^2 )) =1−4(√(t/π))+t [ ∫_0 ^∞ t^(1/2) e^(−st) dt=((√π)/(2s^(3/2) ))⇒(2/( (√π)))L((√t))=(1/( (√s^3 )))]](Q129020.png)
$$\mathscr{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{s}}−\frac{\mathrm{2}}{\:{s}^{\frac{\mathrm{3}}{\mathrm{2}}} }+\frac{\mathrm{1}}{{s}^{\mathrm{2}} }\right) \\ $$$$=\mathrm{1}−\mathrm{4}\sqrt{\frac{{t}}{\pi}}+{t}\:\:\:\:\:\:\:\:\:\:\left[\:\:\int_{\mathrm{0}} ^{\infty} {t}^{\frac{\mathrm{1}}{\mathrm{2}}} {e}^{−{st}} {dt}=\frac{\sqrt{\pi}}{\mathrm{2}{s}^{\frac{\mathrm{3}}{\mathrm{2}}} }\Rightarrow\frac{\mathrm{2}}{\:\sqrt{\pi}}\mathscr{L}\left(\sqrt{{t}}\right)=\frac{\mathrm{1}}{\:\sqrt{{s}^{\mathrm{3}} }}\right] \\ $$
Commented by BHOOPENDRA last updated on 12/Jan/21
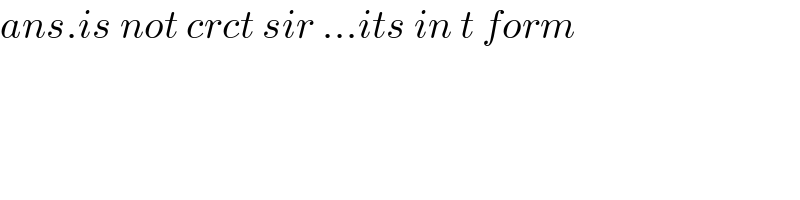
$${ans}.{is}\:{not}\:{crct}\:{sir}\:...{its}\:{in}\:{t}\:{form} \\ $$
Commented by Dwaipayan Shikari last updated on 12/Jan/21
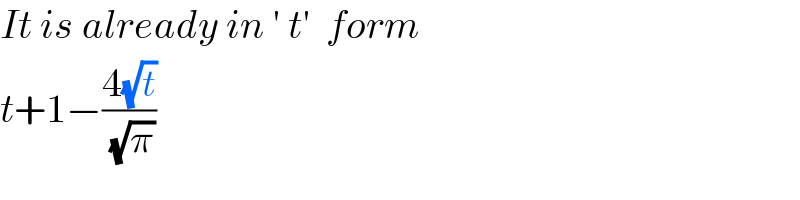
$${It}\:{is}\:{already}\:{in}\:'\:{t}'\:\:{form} \\ $$$${t}+\mathrm{1}−\frac{\mathrm{4}\sqrt{{t}}}{\:\sqrt{\pi}} \\ $$
Commented by BHOOPENDRA last updated on 12/Jan/21
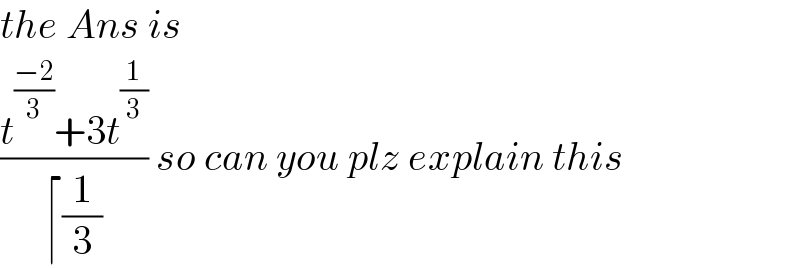
$${the}\:{Ans}\:{is}\: \\ $$$$\frac{{t}^{\frac{−\mathrm{2}}{\mathrm{3}}} +\mathrm{3}{t}^{\frac{\mathrm{1}}{\mathrm{3}}} }{\lceil\frac{\mathrm{1}}{\mathrm{3}}}\:{so}\:{can}\:{you}\:{plz}\:{explain}\:{this} \\ $$
Commented by Dwaipayan Shikari last updated on 12/Jan/21
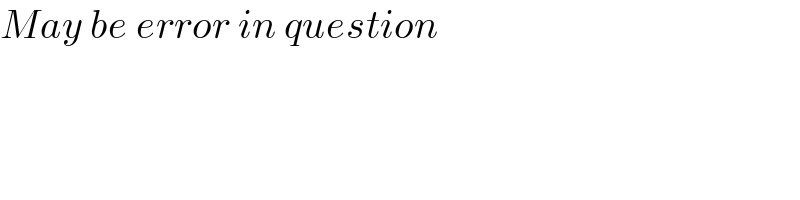
$${May}\:{be}\:{error}\:{in}\:{question}\: \\ $$
