
Question Number 208420 by lepuissantcedricjunior last updated on 15/Jun/24
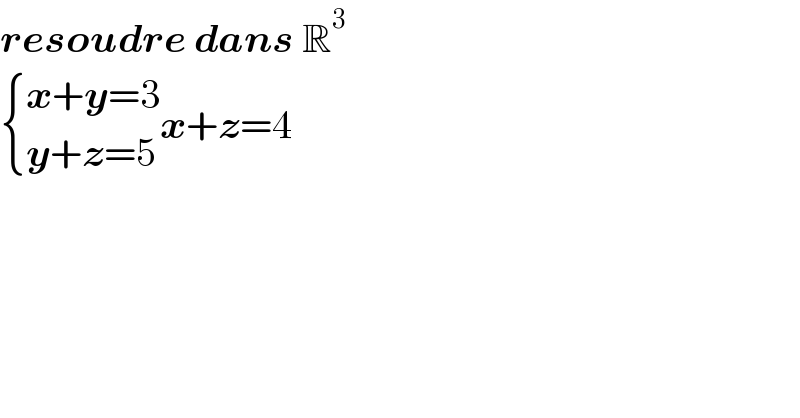
$$\boldsymbol{{resoudre}}\:\boldsymbol{{dans}}\:\mathbb{R}^{\mathrm{3}} \\ $$$$\begin{cases}{\boldsymbol{{x}}+\boldsymbol{{y}}=\mathrm{3}}\\{\boldsymbol{{y}}+\boldsymbol{{z}}=\mathrm{5}}\end{cases}\boldsymbol{{x}}+\boldsymbol{{z}}=\mathrm{4} \\ $$
Commented by A5T last updated on 15/Jun/24
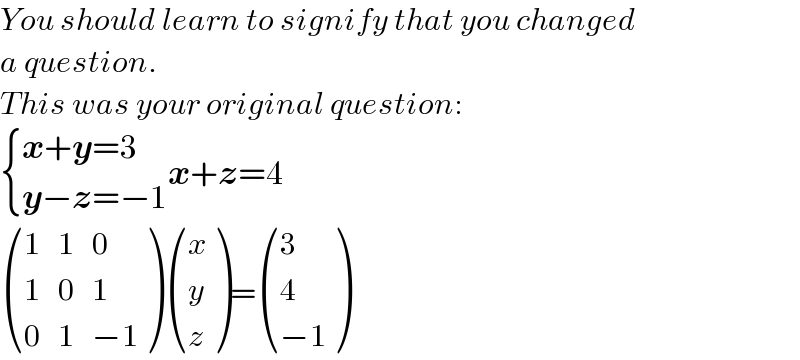
$${You}\:{should}\:{learn}\:{to}\:{signify}\:{that}\:{you}\:{changed} \\ $$$${a}\:{question}. \\ $$$${This}\:{was}\:{your}\:{original}\:{question}: \\ $$$$\begin{cases}{\boldsymbol{{x}}+\boldsymbol{{y}}=\mathrm{3}}\\{\boldsymbol{{y}}−\boldsymbol{{z}}=−\mathrm{1}}\end{cases}\boldsymbol{{x}}+\boldsymbol{{z}}=\mathrm{4} \\ $$$$\begin{pmatrix}{\mathrm{1}}&{\mathrm{1}}&{\mathrm{0}}\\{\mathrm{1}}&{\mathrm{0}}&{\mathrm{1}}\\{\mathrm{0}}&{\mathrm{1}}&{−\mathrm{1}}\end{pmatrix}\begin{pmatrix}{{x}}\\{{y}}\\{{z}}\end{pmatrix}=\begin{pmatrix}{\mathrm{3}}\\{\mathrm{4}}\\{−\mathrm{1}}\end{pmatrix} \\ $$
Answered by A5T last updated on 15/Jun/24
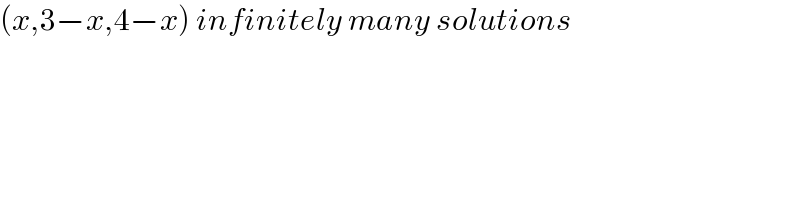
$$\left({x},\mathrm{3}−{x},\mathrm{4}−{x}\right)\:{infinitely}\:{many}\:{solutions} \\ $$
Commented by A5T last updated on 15/Jun/24
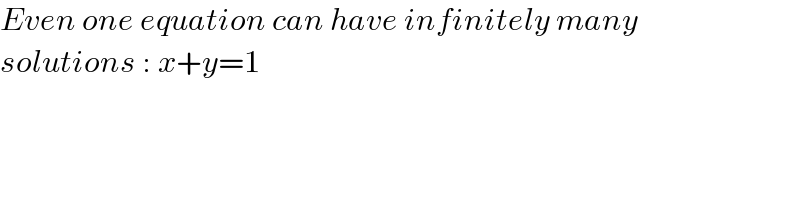
$${Even}\:{one}\:{equation}\:{can}\:{have}\:{infinitely}\:{many}\: \\ $$$${solutions}\::\:{x}+{y}=\mathrm{1} \\ $$
Commented by lepuissantcedricjunior last updated on 15/Jun/24

$${no}!!! \\ $$$$\boldsymbol{{c}}'{est}\:\boldsymbol{{trois}}\:\boldsymbol{{equations}} \\ $$
Answered by Frix last updated on 15/Jun/24

$$\mathrm{1}+\mathrm{2}=\mathrm{3} \\ $$$$\mathrm{1}+\mathrm{3}=\mathrm{4} \\ $$$$\mathrm{2}+\mathrm{3}=\mathrm{5} \\ $$$${x}=\mathrm{1}\:{y}=\mathrm{2}\:{z}=\mathrm{3} \\ $$
