
Question Number 183563 by CrispyXYZ last updated on 27/Dec/22

$$\mathrm{repost}\:\mathrm{an}\:\mathrm{unsolved}\:\mathrm{question}\:\mathrm{Q182552} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{period}\:\mathrm{of}\:\mathrm{the}\:\mathrm{following}: \\ $$$$\:{a}\bullet\:\mathrm{sin}\:\mathrm{4}{x}\:\mathrm{sin}\:\mathrm{3}{x} \\ $$$$\:{b}\bullet\:\mathrm{sin}\:\pi{x}+\:\mathrm{cos}\:{x} \\ $$$$\:{c}\bullet\:\frac{\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{3}{x}−\:\mathrm{3}\:\mathrm{tan}\:\mathrm{4}{x}+\:\mathrm{4}\:\mathrm{cot}\:\mathrm{6}{x}}{\mid\mathrm{cosec}\:\mathrm{8}{x}\mid−\:\mathrm{sec}^{\mathrm{3}} \:\mathrm{10}{x}+\:\sqrt{\mathrm{cot}\:\mathrm{12}{x}}} \\ $$
Commented by Acem last updated on 27/Dec/22
$${Thanks}\:{friend}\:{for}\:{reminding}\:{us}\:{this}\:{question}, \\ $$$$\:{hope}\:{from}\:{all}\:{sharing}\:{their}\:{methodes}. \\ $$
Answered by mr W last updated on 27/Dec/22
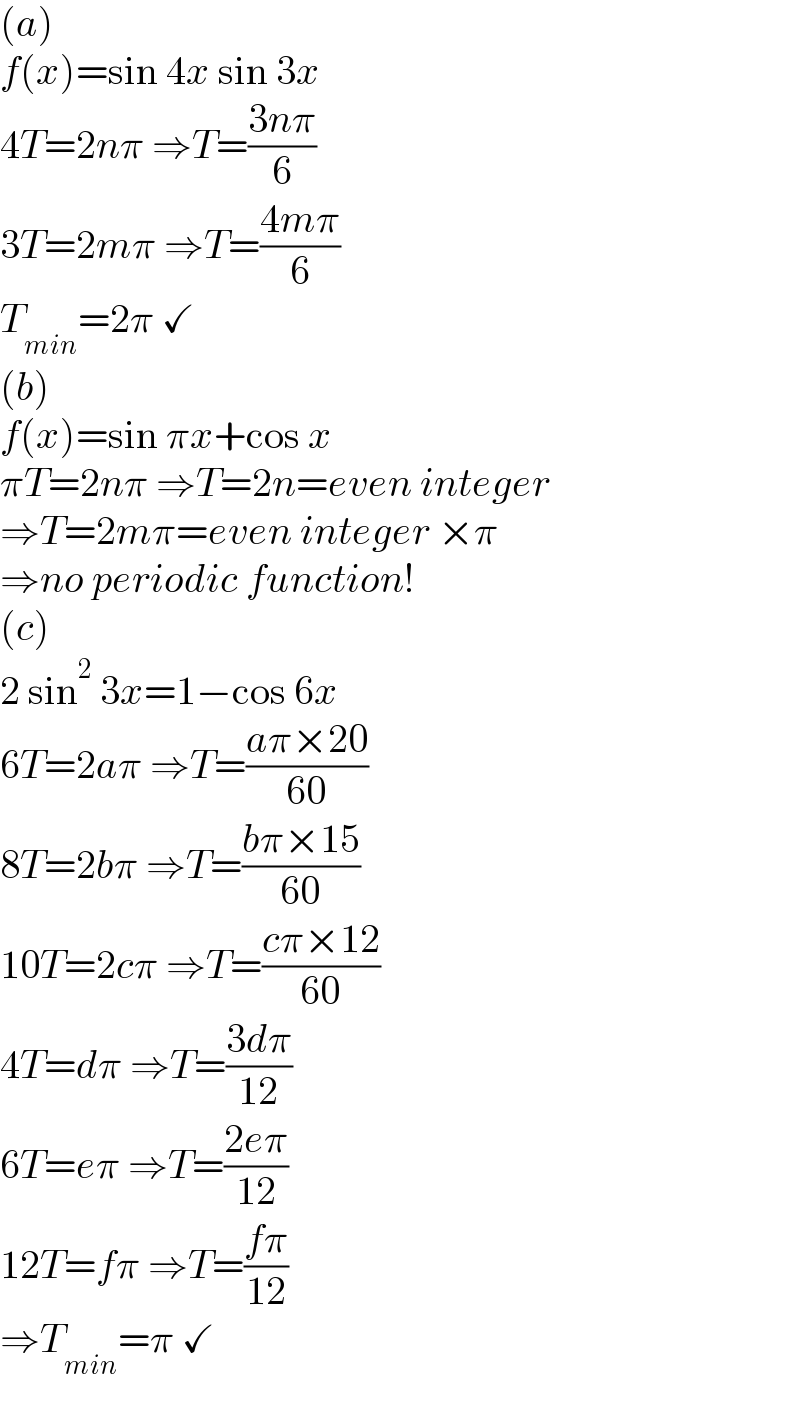
$$\left({a}\right) \\ $$$${f}\left({x}\right)=\mathrm{sin}\:\mathrm{4}{x}\:\mathrm{sin}\:\mathrm{3}{x} \\ $$$$\mathrm{4}{T}=\mathrm{2}{n}\pi\:\Rightarrow{T}=\frac{\mathrm{3}{n}\pi}{\mathrm{6}} \\ $$$$\mathrm{3}{T}=\mathrm{2}{m}\pi\:\Rightarrow{T}=\frac{\mathrm{4}{m}\pi}{\mathrm{6}} \\ $$$${T}_{{min}} =\mathrm{2}\pi\:\checkmark \\ $$$$\left({b}\right) \\ $$$${f}\left({x}\right)=\mathrm{sin}\:\pi{x}+\mathrm{cos}\:{x} \\ $$$$\pi{T}=\mathrm{2}{n}\pi\:\Rightarrow{T}=\mathrm{2}{n}={even}\:{integer} \\ $$$$\Rightarrow{T}=\mathrm{2}{m}\pi={even}\:{integer}\:×\pi \\ $$$$\Rightarrow{no}\:{periodic}\:{function}! \\ $$$$\left({c}\right) \\ $$$$\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{3}{x}=\mathrm{1}−\mathrm{cos}\:\mathrm{6}{x} \\ $$$$\mathrm{6}{T}=\mathrm{2}{a}\pi\:\Rightarrow{T}=\frac{{a}\pi×\mathrm{20}}{\mathrm{60}} \\ $$$$\mathrm{8}{T}=\mathrm{2}{b}\pi\:\Rightarrow{T}=\frac{{b}\pi×\mathrm{15}}{\mathrm{60}} \\ $$$$\mathrm{10}{T}=\mathrm{2}{c}\pi\:\Rightarrow{T}=\frac{{c}\pi×\mathrm{12}}{\mathrm{60}} \\ $$$$\mathrm{4}{T}={d}\pi\:\Rightarrow{T}=\frac{\mathrm{3}{d}\pi}{\mathrm{12}} \\ $$$$\mathrm{6}{T}={e}\pi\:\Rightarrow{T}=\frac{\mathrm{2}{e}\pi}{\mathrm{12}} \\ $$$$\mathrm{12}{T}={f}\pi\:\Rightarrow{T}=\frac{{f}\pi}{\mathrm{12}} \\ $$$$\Rightarrow{T}_{{min}} =\pi\:\checkmark \\ $$
