Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 194559 by MM42 last updated on 09/Jul/23

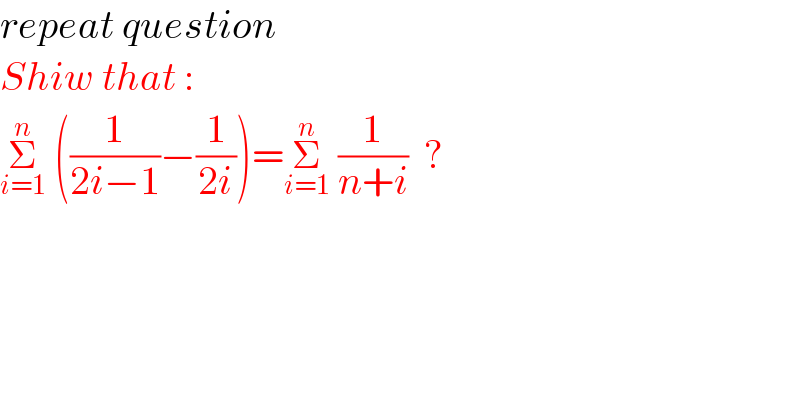
repeat question Shiw that : Σ_(i=1) ^n ((1/(2i−1))−(1/(2i)))=Σ_(i=1) ^n (1/(n+i)) ?

$${repeat}\:{question} \\ $$$${Shiw}\:{that}\:: \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\:\left(\frac{\mathrm{1}}{\mathrm{2}{i}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{i}}\right)=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\mathrm{1}}{{n}+{i}}\:\:? \\ $$

Answered by witcher3 last updated on 10/Jul/23

n=1⇒1−(1/2)=(1/2)=(1/(1+1)) ∀n∈Z_+ suppose TrueΣ_(i=1) ^n (1/(2i−1))−(1/(2i))=Σ(1/(n+i)) Σ_(i=1) ^(n+1) (1/(2i−1))−(1/(2i))=^? Σ_(i=1) ^n (1/(n+1+i))=Σ_(i=1) ^(n−1) (1/(n+1+i))+(1/(2n+1)) ⇔Σ_(i=1) ^n ((1/(2i−1))−(1/(2i)))+(1/(2n+1))−(1/(2n+2))= Σ_(i=1) ^n (1/(n+i))+(1/(2n+1))−(1/(2n+2))=Σ_(n=2) ^n (1/(n+i))+(1/(2n+1))+(1/(n+1))−(1/(2(n+1))) =Σ_(i=1) ^(n−1) (1/(n+1+i))+(1/(n+1+n))+(1/(n+1+n+1)) =Σ_(i=1) ^(n+1) (1/((n+1)+i))....True

$$\mathrm{n}=\mathrm{1}\Rightarrow\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{1}} \\ $$$$\forall\mathrm{n}\in\mathbb{Z}_{+} \mathrm{suppose}\:\mathrm{True}\underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2i}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{\mathrm{i}}}=\Sigma\frac{\mathrm{1}}{\mathrm{n}+\mathrm{i}} \\ $$$$\underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{n}+\mathrm{1}} {\sum}}\frac{\mathrm{1}}{\mathrm{2i}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2i}}\overset{?} {=}\underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}+\mathrm{i}}=\underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}+\mathrm{i}}+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}} \\ $$$$\Leftrightarrow\underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2i}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2i}}\right)+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{2}}= \\ $$$$\underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{i}}+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{2}}=\underset{\mathrm{n}=\mathrm{2}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{i}}+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)} \\ $$$$=\underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}+\mathrm{i}}+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}+\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}+\mathrm{n}+\mathrm{1}} \\ $$$$=\underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{n}+\mathrm{1}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{i}}....\mathrm{True} \\ $$$$ \\ $$

Commented by MM42 last updated on 10/Jul/23

excellent ★

$${excellent}\:\:\bigstar \\ $$

Commented by witcher3 last updated on 11/Jul/23

thank You sir

$$\mathrm{thank}\:\mathrm{You}\:\mathrm{sir} \\ $$

Answered by MM42 last updated on 10/Jul/23

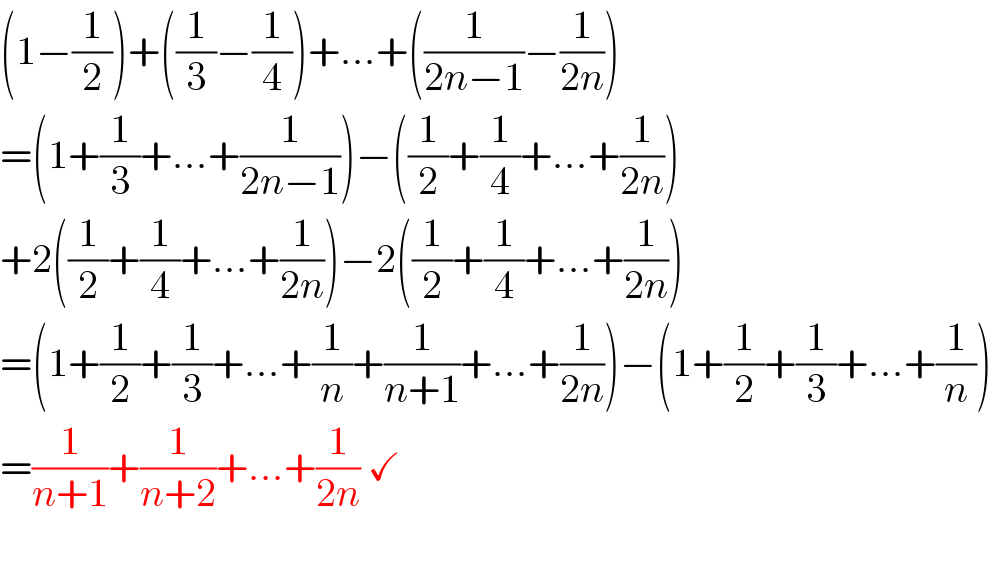
(1−(1/2))+((1/3)−(1/4))+...+((1/(2n−1))−(1/(2n))) =(1+(1/3)+...+(1/(2n−1)))−((1/2)+(1/4)+...+(1/(2n))) +2((1/2)+(1/4)+...+(1/(2n)))−2((1/2)+(1/4)+...+(1/(2n))) =(1+(1/2)+(1/3)+...+(1/n)+(1/(n+1))+...+(1/(2n)))−(1+(1/2)+(1/3)+...+(1/n)) =(1/(n+1))+(1/(n+2))+...+(1/(2n)) ✓

$$\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}\right)+...+\left(\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{n}}\right) \\ $$$$=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+...+\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}\right)−\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+...+\frac{\mathrm{1}}{\mathrm{2}{n}}\right) \\ $$$$+\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+...+\frac{\mathrm{1}}{\mathrm{2}{n}}\right)−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+...+\frac{\mathrm{1}}{\mathrm{2}{n}}\right) \\ $$$$=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+...+\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}+\mathrm{1}}+...+\frac{\mathrm{1}}{\mathrm{2}{n}}\right)−\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+...+\frac{\mathrm{1}}{{n}}\right) \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}+\mathrm{2}}+...+\frac{\mathrm{1}}{\mathrm{2}{n}}\:\checkmark \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com